تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Rotation of a rigid body
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 18
2024-02-29
1707
Now let us discuss rotations. Of course, an ordinary object does not simply rotate, it wobbles, shakes, and bends, so to simplify matters we shall discuss the motion of a nonexistent ideal object which we call a rigid body. This means an object in which the forces between the atoms are so strong, and of such character, that the little forces that are needed to move it do not bend it. Its shape stays essentially the same as it moves about. If we wish to study the motion of such a body, and agree to ignore the motion of its center of mass, there is only one thing left for it to do, and that is to turn. We have to describe that. How? Suppose there is some line in the body which stays put (perhaps it includes the center of mass and perhaps not), and the body is rotating about this particular line as an axis. How do we define the rotation? That is easy enough, for if we mark a point somewhere on the object, anywhere except on the axis, we can always tell exactly where the object is, if we only know where this point has gone to. The only thing needed to describe the position of that point is an angle. So rotation consists of a study of the variations of the angle with time.
In order to study rotation, we observe the angle through which a body has turned. Of course, we are not referring to any particular angle inside the object itself; it is not that we draw some angle on the object. We are talking about the angular change of the position of the whole thing, from one time to another.
First, let us study the kinematics of rotations. The angle will change with time, and just as we talked about position and velocity in one dimension, we may talk about angular position and angular velocity in plane rotation. In fact, there is a very interesting relationship between rotation in two dimensions and one-dimensional displacement, in which almost every quantity has its analog. First, we have the angle θ which defines how far the body has gone around; this replaces the distance s, which defines how far it has gone along. In the same manner, we have a velocity of turning, ω=dθ/dt, which tells us how much the angle changes in a second, just as v=ds/dt describes how fast a thing moves, or how far it moves in a second. If the angle is measured in radians, then the angular velocity ω will be so and so many radians per second. The greater the angular velocity, the faster the object is turning, the faster the angle changes. We can go on: we can differentiate the angular velocity with respect to time, and we can call α= dω/dt= d2θ/dt2 the angular acceleration. That would be the analog of the ordinary acceleration.
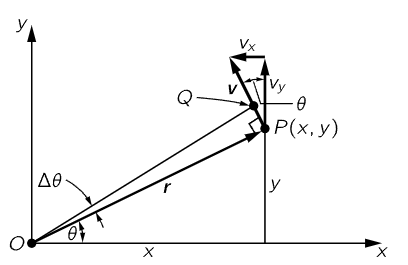
Fig. 18–1. Kinematics of two-dimensional rotation.
Now of course we shall have to relate the dynamics of rotation to the laws of dynamics of the particles of which the object is made, so we must find out how a particular particle moves when the angular velocity is such and such. To do this, let us take a certain particle which is located at a distance r from the axis and say it is in a certain location P(x,y) at a given instant, in the usual manner (Fig. 18–1). If at a moment Δt later the angle of the whole object has turned through Δθ, then this particle is carried with it. It is at the same radius away from O as it was before, but is carried to Q. The first thing we would like to know is how much the distance x changes and how much the distance y changes. If OP is called r, then the length PQ is r Δθ, because of the way angles are defined. The change in x, then, is simply the projection of r Δθ in the x-direction:
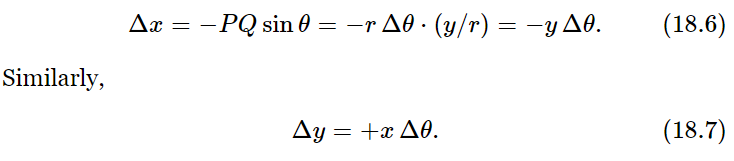
If the object is turning with a given angular velocity ω, we find, by dividing both sides of (18.6) and (18.7) by Δt, that the velocity of the particle is
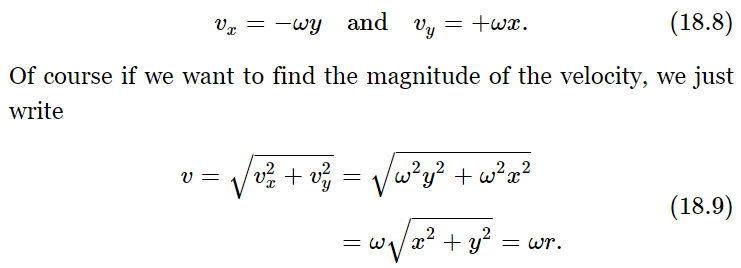
It should not be mysterious that the value of the magnitude of this velocity is ωr; in fact, it should be self-evident, because the distance that it moves is rΔθ and the distance it moves per second is r Δθ/Δt, or rω.
Let us now move on to consider the dynamics of rotation. Here a new concept, force, must be introduced. Let us inquire whether we can invent something which we shall call the torque (L. torquers, to twist) which bears the same relationship to rotation as force does to linear movement. A force is the thing that is needed to make linear motion, and the thing that makes something rotate is a “rotary force” or a “twisting force,” i.e., a torque. Qualitatively, a torque is a “twist”; what is a torque quantitatively? We shall get to the theory of torques quantitatively by studying the work done in turning an object, for one very nice way of defining a force is to say how much work it does when it acts through a given displacement. We are going to try to maintain the analogy between linear and angular quantities by equating the work that we do when we turn something a little bit when there are forces acting on it, to the torque times the angle it turns through. In other words, the definition of the torque is going to be so arranged that the theorem of work has an absolute analog: force times distance is work, and torque times angle is going to be work. That tells us what torque is. Consider, for instance, a rigid body of some kind with various forces acting on it, and an axis about which the body rotates. Let us at first concentrate on one force and suppose that this force is applied at a certain point (x,y). How much work would be done if we were to turn the object through a very small angle? That is easy. The work done is
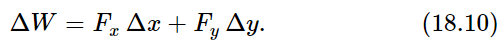
We need only to substitute Eqs. (18.6) and (18.7) for Δx and Δy to obtain
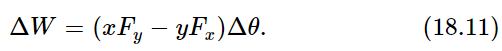
That is, the amount of work that we have done is, in fact, equal to the angle through which we have turned the object, multiplied by a strange-looking combination of the force and the distance. This “strange combination” is what we call the torque. So, defining the change in work as the torque times the angle, we now have the formula for torque in terms of the forces. (Obviously, torque is not a completely new idea independent of Newtonian mechanics—torque must have a definite definition in terms of the force.)
When there are several forces acting, the work that is done is, of course, the sum of the works done by all the forces, so that ΔW will be a whole lot of terms, all added together, for all the forces, each of which is proportional, however, to Δθ. We can take the Δθ outside and therefore can say that the change in the work is equal to the sum of all the torques due to all the different forces that are acting, times Δθ. This sum we might call the total torque, τ. Thus, torques add by the ordinary laws of algebra, but we shall later see that this is only because we are working in a plane. It is like one-dimensional kinematics, where the forces simply add algebraically, but only because they are all in the same direction. It is more complicated in three dimensions. Thus, for two-dimensional rotation,
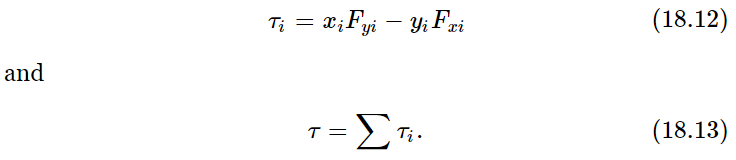
It must be emphasized that the torque is about a given axis. If a different axis is chosen, so that all the xi and yi are changed, the value of the torque is (usually) changed too.
Now we pause briefly to note that our foregoing introduction of torque, through the idea of work, gives us a most important result for an object in equilibrium: if all the forces on an object are in balance both for translation and rotation, not only is the net force zero, but the total of all the torques is also zero, because if an object is in equilibrium, no work is done by the forces for a small displacement. Therefore, since ΔW=τ Δθ=0, the sum of all the torques must be zero. So there are two conditions for equilibrium: that the sum of the forces is zero, and that the sum of the torques is zero. Prove that it suffices to be sure that the sum of torques about any one axis (in two dimensions) is zero.
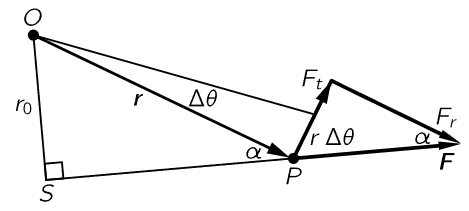
Fig. 18–2. The torque produced by a force.
Now let us consider a single force, and try to figure out, geometrically, what this strange thing xFy−yFx amounts to. In Fig. 18–2 we see a force F acting at a point r. When the object has rotated through a small angle Δθ, the work done, of course, is the component of force in the direction of the displacement times the displacement. In other words, it is only the tangential component of the force that counts, and this must be multiplied by the distance r Δθ. Therefore, we see that the torque is also equal to the tangential component of force (perpendicular to the radius) times the radius. That makes sense in terms of our ordinary idea of the torque, because if the force were completely radial, it would not put any “twist” on the body; it is evident that the twisting effect should involve only the part of the force which is not pulling out from the center, and that means the tangential component. Furthermore, it is clear that a given force is more effective on a long arm than near the axis. In fact, if we take the case where we push right on the axis, we are not twisting at all! So, it makes sense that the amount of twist, or torque, is proportional both to the radial distance and to the tangential component of the force.
There is still a third formula for the torque which is very interesting. We have just seen that the torque is the force times the radius times the sine of the angle α, in Fig. 18–2. But if we extend the line of action of the force and draw the line OS, the perpendicular distance to the line of action of the force (the lever arm of the force) we notice that this lever arm is shorter than r in just the same proportion as the tangential part of the force is less than the total force. Therefore, the formula for the torque can also be written as the magnitude of the force times the length of the lever arm.
The torque is also often called the moment of the force. The origin of this term is obscure, but it may be related to the fact that “moment” is derived from the Latin movimentum, and that the capability of a force to move an object (using the force on a lever or crowbar) increases with the length of the lever arm. In mathematics “moment” means weighted by how far away it is from an axis.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)