Now we must describe the laws, or rules, for combining vectors in various ways. The first such combination is the addition of two vectors: suppose that a is a vector which in some particular coordinate system has the three components (a_x, a_y, a_z), and that b is another vector which has the three components (b_x, b_y, b_z). Now let us invent three new numbers (a_x + b_x, a_y + b_y, a_z + b_z). Do these form a vector? “Well,” we might say, “they are three numbers, and every three numbers form a vector.” No, not every three numbers form a vector! In order for it to be a vector, not only must there be three numbers, but these must be associated with a coordinate system in such a way that if we turn the coordinate system, the three numbers “revolve” on each other, get “mixed up” in each other, by the precise laws we have already described. So, the question is, if we now rotate the coordinate system so that (a_x, a_y, a_z) become (a_x′, a_y′, a_z′) and (b_x, b_y, b_z) become (bx′, by′, bz′), what do (a_x + b_x, a_y + b_y, a_z + b_z) become? Do they become (a_x′ + b_x′, a_y′ + b_y′, a_z′ + b_z′) or not? The answer is, of course, yes, because the prototype transformations of Eq. (11.5) constitute what we call a linear transformation. If we apply those transformations to a_x and b_x to get a_x′ + b_x′, we find that the transformed a_x + b_x is indeed the same as a_x′ + b_x′. When a and b are “added together” in this sense, they will form a vector which we may call c. We would write this as

c = a + b.

Now c has the interesting property

c = b + a,

as we can immediately see from its components. Thus also,

a + (b + c) = (a + b) + c.

We can add vectors in any order.

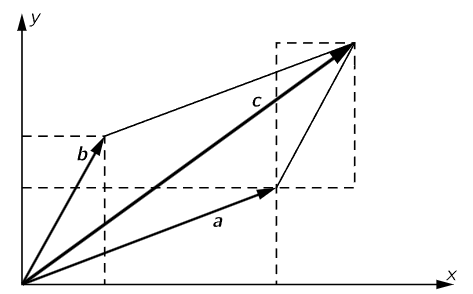
Fig. 11–4. The addition of vectors.

What is the geometric significance of a + b? Suppose that a and b were represented by lines on a piece of paper, what would c look like? This is shown in Fig. 11–4. We see that we can add the components of b to those of a most conveniently if we place the rectangle representing the components of b next to that representing the components of a in the manner indicated. Since b just “fits” into its rectangle, as does a into its rectangle, this is the same as putting the “tail” of b on the “head” of a, the arrow from the “tail” of a to the “head” of b being the vector c. Of course, if we added a to b the other way around, we would put the “tail” of a on the “head” of b, and by the geometrical properties of parallelograms we would get the same result for c. Note that vectors can be added in this way without reference to any coordinate axes.

Suppose we multiply a vector by a number α, what does this mean? We define it to mean a new vector whose components are αa_x, αa_y, and αa_z. We leave it as a problem for the student to prove that it is a vector.

Now let us consider vector subtraction. We may define subtraction in the same way as addition, but instead of adding, we subtract the components. Or we might define subtraction by defining a negative vector, −b = −1b, and then we would add the components. It comes to the same thing. The result is shown in Fig. 11–5. This figure shows d = a − b= a + (−b); we also note that the difference a − b can be found very easily from a and b by using the equivalent relation a = b + d. Thus, the difference is even easier to find than the sum: we just draw the vector from b to a, to get a − b!

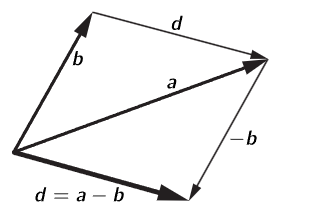
Fig. 11–5. The subtraction of vectors.

Next, we discuss velocity. Why is velocity a vector? If position is given by the three coordinates (x, y, z), what is the velocity? The velocity is given by dx/dt, dy/dt, and dz/dt. Is that a vector, or not? We can find out by differentiating the expressions in Eq. (11.5) to find out whether dx′/dt transforms in the right way. We see that the components dx/dt and dy/dt do transform according to the same law as x and y, and therefore the time derivative is a vector. So, the velocity is a vector. We can write the velocity in an interesting way as

v = dr/dt.

What the velocity is, and why it is a vector, can also be understood more pictorially: How far does a particle move in a short time Δt? Answer: Δr, so if a particle is “here” at one instant and “there” at another instant, then the vector difference of the positions Δr = r₂ − r₁, which is in the direction of motion shown in Fig. 11–6, divided by the time interval Δt=t₂−t₁, is the “average velocity” vector.

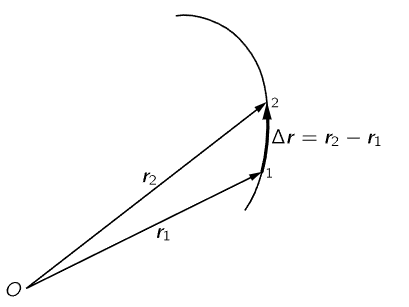
Fig. 11–6. The displacement of a particle in a short time interval Δt=t₂−t₁.

In other words, by vector velocity we mean the limit, as Δt goes to 0, of the difference between the radius vectors at the time t+Δt and the time t, divided by Δt:

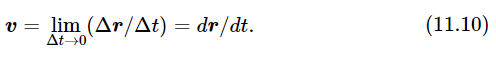
Thus, velocity is a vector because it is the difference of two vectors. It is also the right definition of velocity because its components are dx/dt, dy/dt, and dz/dt. In fact, we see from this argument that if we differentiate any vector with respect to time, we produce a new vector. So, we have several ways of producing new vectors: (1) multiply by a constant, (2) differentiate with respect to time, (3) add or subtract two vectors.