
تحليل التوزيع القطري Radial Distribution Analysis
 المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
 المصدر:
علم البلورات والاشعة السينية
المصدر:
علم البلورات والاشعة السينية
 الجزء والصفحة:
ص399–409
الجزء والصفحة:
ص399–409
 2023-10-10
2023-10-10
 1745
1745
الخلفية النظرية:
وضع ديباي الأسس النظرية لعملية التحليل بالتوزيع القطري حيث أوضح أن شدة التشتت بواسطة صف من الذرات في مادة غير متبلورة عند زاوية θ تعطى بالمعادلة:
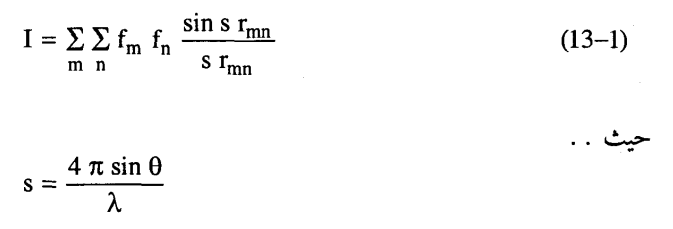
fm ، fn هما معاملا التشتيت الذري للذرات m، n، rmn هو مقدار المتجه الذي يفصل بين الذرتين، وتجري عملية التجميع على كل أزواج الذرات في التركيب.
المعادلة (1-13) يمكن أن تنطبق على صفوف الذرات بافتراض كل الأوضاع في الفراغ وهو ما يتحقق في حالة المواد غير المتبلورة بدون دوران العينة، كما أن هذه المعادلة توضح أنه بالإمكان الوصول إلى الشكل الذري الصحيح وذلك عن طريق مقارنة التشتت العملي مع التشتت النظري المحسوب لعدة أشكال من التركيب الذري، وهذه الطريقة المبنية على التجربة والخطأ اتُّبعت في المراحل الأولى لمثل هذه الدراسات وأدت إلى نجاح بدرجات متفاوتة ولكن بعد ذلك أمكن تطبيق نظرية تكامل فوريير التي اقترحها Fourier integral theorem] Zernicken and Prins] . للحصول على ما يسمى دالة التوزيع القطري (radial – distribution function) للعينة بدون أية افتراضات لتركيبها وتطبيق نظرية تكامل فوريير تتم على الوجه الأكمل بدون عقبات في حالة المواد التي تتكون من نوع واحد من الذرات وعندئذ تصبح المعادلة (1-13) كالآتي:

وهذا إذا افترضنا أن ما يحيط بأي ذرة هو مثل ما يحيط بأي ذرة أخرى وحيث أنه عند إجراء التجميع في المعادلة (2-13) تصبح كل ذرة بدورها ذرة مرجعية فإنه يصبح عندنا عدد N من العناصر في المعادلة نتيجة لتفاعل كل ذرة مع نفسها وتكون قيمة كل عنصر من هذه العناصر هي الوحدة لأنه عندما تؤول rmn إلى الصفر
(0 → Fmn) فإن القيمة ((sin srmn) /(srmn تصبح الوحدة، وعلى هذا فالمعادلة (2-13) يمكن أن تكتب بالشكل الآتي:

وذلك إذا كان التجميع لا يسري على الذرة عند المركز.
والآن يمكن اعتبار أن توزيع الذرات حول ذرة مرجعية يمثل بدالة مستمرة ويمكن استبدال التجميع بالتكامل:
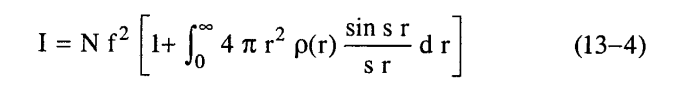
حيث (r)ρ هي عدد الذرات في وحدة الحجوم على مسافة r من الذرة المرجعية
(r)ρ 4π r2 هو عدد الذرات المحتواة في قشرة كروية لها نصف قطر r وسمك dr وإذا كانت ρ0 هي متوسط كثافة الذرات في العينة فإن المعادلة (4-13) يمكن كتابتها على الصورة:
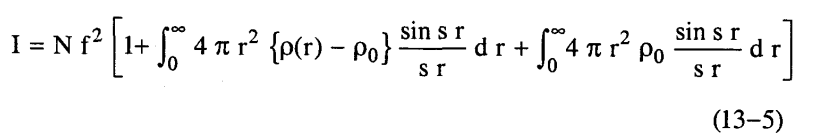
والتكامل الثاني في هذه المعادلة يساوي صفرا إلا إذا كانت s صغيرة جدا حيث تكون شدة الأشعة المشتتة لا يمكن فصلها عن الشعاع الأصلي ولا يمكن مشاهدتها، وعلى هذا فإذا اقتصر الاهتمام على ما نحصل عليه عمليا فإن المعادلة (5-13) تصبح:

وقد كان ديباي ومينك Debye and Menke هما أول من استخدم نظرية تكامل فوريير لدراسة المواد غير المتبلورة التي تتكون من نوع واحد من الذرات وهو الزئبق وبعد ذلك أدخلت تعديلات على المعادلة (1-13) لتصبح صالحة للاستخدام في حالة وجود أكثر من نوع واحد من الذرات ولكي تصبح:
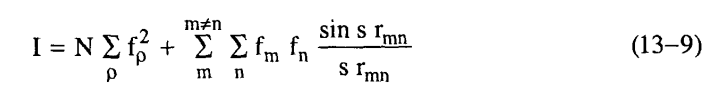
حيث n،m ، ... هي رموز للذرات المختلفة التي تكون وحدة التركيب (جزيء على سبيل المثال) التي تشكل العينة بكاملها، N هو عدد هذه الوحدات. ويسري التجميع الأول على كل الذرات المكونة لوحدة التركيب، أما التجميع الثاني فيسري على كل زوج من الذرات في العينة بصرف النظر عن انتمائهما لوحدة التركيب.
والآن بالنظر إلى توزيع الذرات حول أي ذرة تُؤخذ كمرجع على أنه توزيع مستمر نفترض أن ذرة من النوع m هي الذرة المرجعية وأن متوسط عدد الذرات
من الأنواع m،n ، ... التي توجد في منطقة قشرية دائرية لها نصف قطر r وسمك dr هي am ، an، ... وغيرها.
والآن يمكن أن نُعرف دالة الكثافة ذات الوزن ((ρm (r) كالآتي:

حيث يجري التجميع على كل الذرات في وحدة التركيب التي اختيرت مسبقا وبذلك تصبح المعادلة (9-13) كالآتي:

وإذا افترضنا أن معامل التشتت للذرة m يمكن أن يعبر عنه بدلالة معامل التشتت للإلكترون f كالآتي:

حيث km هو عدد الإلكترونات في الذرة m وهذا يعنى الافتراض أن تغير f مع الزاوية θ (زاوية الحيود أو التشتت) هو تغير واحد لكل الذرات، وهذا يعتبر تقريبا مقبولا للذرات التي لا تختلف اختلافا كبيرا في عددها الذري ودالة الكثافة الذرية (r)ρm في المعادلة (10-13) يمكن الآن أن يعبر عنها بدلالة fe كالآتي:

(gm (r هي دالة الكثافة الإلكترونية.
وبالتعويض من المعادلتين (12-13)، (13-13) في المعادلة (11-13) نحصل على:

وبالمثل في حالة اشتقاق المعادلة (6-13) من (4-13) فالمعادلة (14-13) يمكن أن
تصير کالاتي:

وبتطبيق نظرية تكامل فوريير نحصل على:

وفي هذه المعادلة Zn تكون هي العدد الذرى للذرات من النوع m.
تعيين دالة التوزيع القطري باستخدام المعادلة (17-13) أو (16-13) يتم على مرحلتين أولهما التقييم العددي للدالة (i (s من البيانات العملية وثانيتهما الحساب العددي للتكامل:
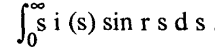
ومن ناحية المبدأ تنطبق المعادلتان على التشتت الذاتي وغير الذاتي ويمتد التكامل في هاتين المعادلتين لقيم كبيرة للكمية s كما أن تكامل المعادلة (14-13) يقترب من الصفر كلما كبرت قيمة s، وبذلك فإن شدة الأشعة الذاتية المشتتة (I (coherent تقترب من قيمة الأشعة المستقلة الذاتية المشتتة (Nf2 (independent coherent scattering عند القيم الكبيرة للكمية s وهذا يبدو واضحا في شكل (13-14) عند مقارنة المنحني العملي (A) بالمنحني (B) للأشعة المستقلة الذاتية المشتتة لمادة البولي أيزوبرين ونعني بالتشتت المستقل الذاتي التشتت النظري ((hypothetical من مجموعة من الذرات عندما تقوم كل ذرة بتشتيت الأشعة منفردة (غير معتمدة على باقي الذرات) وبذلك لا يحدث تداخل بين الموجات، ومن الواضح أن مجموع التشتت الذاتي المستقل الحادث من عدد N من الذرات التي لها معامل تشتت ذري fm سيكون مساويا للكمية Nfm2 من وحدات الإلكترون (انظر الشكل D الذي يوضح المنحني لقيمة 1 = N).
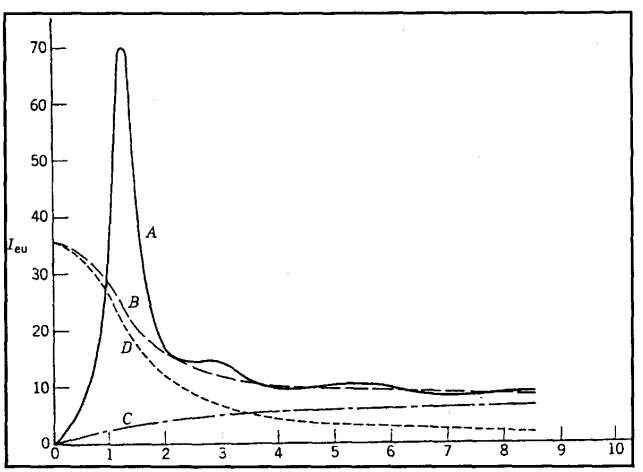
شكل (13-14)
منحني التشتت العملي والمستقل لاحد العينات التشتت العملي (A). التشتت العملي الكلى (B). التشتت غير الذاتي (C). التشتت المستقل الذاتي (D) وبجمع التشتت الذاتي (D) على التشتت غير الذاتي المستقل نحصل على التشتت غير المستقل (B). وعمليا يكفي أن تقاس زاوية التشتت للحد الذي تكون فيه كبيرة بدرجة كافية تجعل (i(s تصل للصفر وفي معظم المواد غير المتبلورة نصل إلى هذه الحالة عندما تصل قيمة s إلى 8 أو 10.
وفي العادة تستخدم أشعة ذات طول موجة قصير مثل αMo K لتعطينا أشعة حيود لها قيمة كبيرة لـ s وللحصول على الأشعة ذات القيم الصغيرة لـ s تستخدم أشعة ذات طول موجة كبير وهذا يكون أفضل وذلك للحصول على تفريق كبير.
بالنظر للمعادلتين (8-13)، (17-13) نلاحظ أن I يجب أن تكون وحداتها مثل وحدات Nf2 أو 
وهذا يمكن إحرازه بمقارنة منحني التشتت العملي الذي يمثل التشتت الذاتي وغير الذاتي والمنحني النظري عند القيم الكبيرة لـ S وبعد ذلك يطرح التشتت النظري غير الذاتي من المنحني العملي وبذلك يبقي التشتت الذاتي المرغوب فيه تفسيرا لطريقة التصحيح للتشتت غير الذاتي تفترض أن شدة الأشعة المشتتة الكلية ذاتية وغير ذاتية بواسطة ذرة عددها الذري Z هي:

حيث Ie هو تشتت الالكترون الواحد، fn هو معامل التشتت للالكترون n في الذرة، R هو معامل الارتداد الذي يمكن أن يعطي قيمة مقدارها الواحد بدون خطأ كبير إلا في حالة المواد ذات العدد الذري المنخفض القيم  تمثل التشتت الذاتي وغير الذاتي للذرة. إذا افترضنا أن Ie تساوي الوحدة فإن كلا النوعين من التشتت يكون بالوحدات الإلكترونية.
تمثل التشتت الذاتي وغير الذاتي للذرة. إذا افترضنا أن Ie تساوي الوحدة فإن كلا النوعين من التشتت يكون بالوحدات الإلكترونية.
منحني شدة الأشعة المقاس لا يمكن مقارنته بالمنحني النظري إلا بعد تصحيحه لأي تشوهات تتغير زاوية التشتت مثل الامتصاص والاستقطاب فالشعاع وحيد الموجة المشتت بواسطة عينة ما تقل شدته بالمعامل.

حيث 'θ هي زاوية براج لمستوى الانعكاس.
وتصحيح شدة الأشعة المشتتة نتيجة عامل الامتصاص يمكن إهماله في حالة المواد العضوية عند استخدام أشعة شديدة النفاذية قصيرة الموجة (مثل αMo k).
مثال عملي
دراسة تركيب الكربون الأسود كانت أول الدراسات التي أجريت باستخدام هذه الطريقة حيث أوضحت هذه الدراسات بواسطة وارين أن مادة الكربون ليست مادة غير متبلورة ولكنها تحتوي على مستويات من الجرافيت.
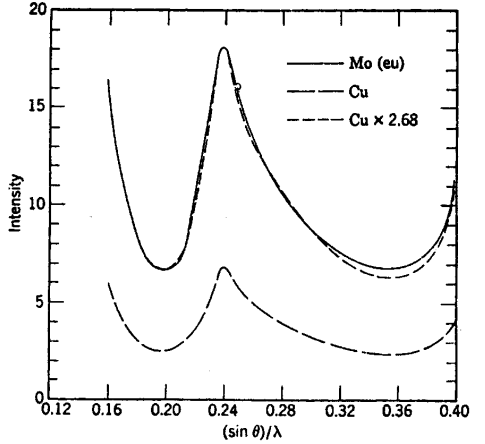
شكل (15-13)
تسوية منحني التشتت من اشعة النحاس بذلك الناتج من اشعة الموليبدنيوم
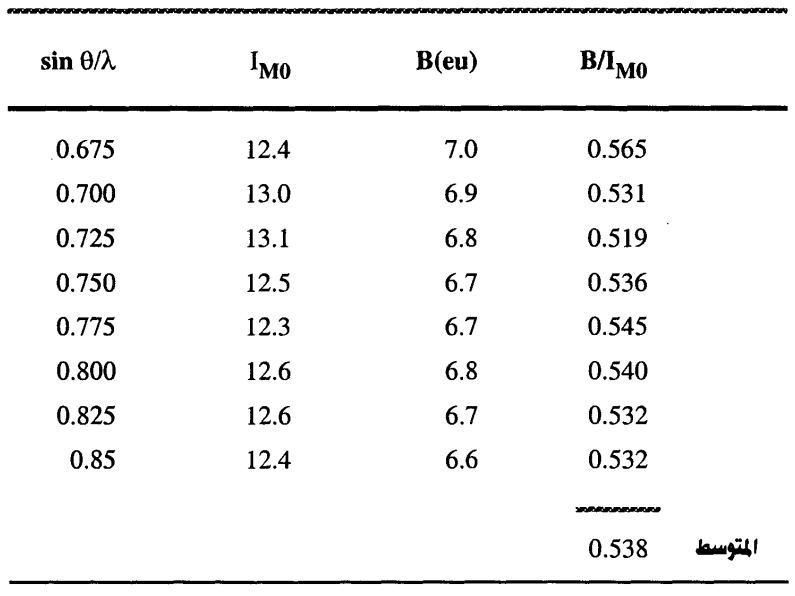
يوضح شكل (13-15) شدة أشعة الموليبدينوم المشتتة بعد إجراء التصويبات عليها كدالة في λ/θsin باستخدام المعادلة (1-13) وبمقارنة المنحنيات B في المنطقة من 0.675 = λ/θsin إلى 0.85 = λ/θsin يمكن استنتاج معامل التحويل لشدة أشعة التشتت للموليبدينوم إلى الوحدات الإلكترونية (electron units) كما هو موضح بالجدول (1-13) وشدة الأشعة المشتتة من أنبوبة الموليبدينوم تستخدم بعد ذلك للحصول على معامل التحويل لشدة الأشعة المشتتة من أنبوبة النحاس إلى الوحدات الإلكترونية وذلك بإيجاد حاصل ضربها في المعامل 0.538 وإعادة رسمها مع منحني النتائج الخاص بأشعة النحاس.
وبيانات شدة التشتت للنوعين من الأشعة أعطت نتائج جيدة في المنطقة من 0.16 = λ/θsin إلى 0.40 = λ/θsin ولذلك فقد استقر الرأي على مقارنة شدة الأشعة المشتتة من أنبوبة الموليبدينوم وأنبوبة النحاس عند قيم صغيرة للفواصل intervals في هذا المدى للوصول لمعامل التسوية normalizing factor الأمثل. ويوضح شكل (13-15) شدة الأشعة من أنبوبة النحاس بعد عملية التسوية لوحدات الإلكترون بمعامل 2.68 أما الشكل (13-16) فيعطي الشكل النهائي لمنحني شدة الأشعة (A) بالوحدات الإلكترونية من كلا النوعين من الأشعة وللمقارنة يوضح الشكل منحنيات التشتت النظرية المستقلة للكربون [المنحني الذاتي (D) والمنحني غير الذاتي (C) ومجموعهما (B)].
جدول (1-13)
استنتاج معامل التحويل لشدة اشعة التشتت للموليدنوم إلى الوحدات الإلكترونية

شكل (13-16)
منحني التشتت من الكربون (A) مقارنا بالمنحنيات المستقلة النظرية الذاتي (D)، غير الذاتي (C). التشتت المستقل الكلي (B)
والبيانات العددية المطلوبة يمكن تفهمها من المعادلة (8-13)، بدلالة دوال التشتت المستقل B،C ،D ، للمنحنيات (14-13)، (16-13).

تختار قيمة sΔ بحيث تكون صغيرة بمقدار كاف لإظهار تفاصيل منحني السعة (Si(s ومعظم المواد غير المتبلورة تكون قيمة 0.10 ≈sΔ مناسبة لإظهار كل التفاصيل اللازمة كما أنها تسمح بحساب قيمة r عند فواصل لا تتعدى 4 أو 5، وللحصول على تفرقة جيدة عند قيم r الكبيرة يجب أن تقل قيمة sΔ إلى حوالي 0.05.
والطريقة الوحيدة لزيادة عدد قيم r المحسوبة لزيادة التفاصيل لدالة التوزيع القطري تكون بزيادة عدد أقسام الدورة.
أما الكثافة الذرية 0ρ في المعادلة (7-13) فإنه يمكن حسابها من الكثافة المشاهدة عمليا للمادة الصلبة بواسطة العلاقة.

حيث d هي الكثافة بالجرامسم3، N عدد أفوجادرو، A الوزن الذري فإذا اعتبرنا أن كثافة الكربون gm/cc2.25 فإن قيمة 0ρ تساوي:

الخط المتصل في الشكل (18-13) هو دالة التوزيع القطري للكربون كما حسبت بالمعادلة (21-13) باستخدام كل بيانات السعة المأخوذة من الشكل (13-17) أما المنحني النقطي فهو يمثل متوسط التوزيع الذري في العينة.
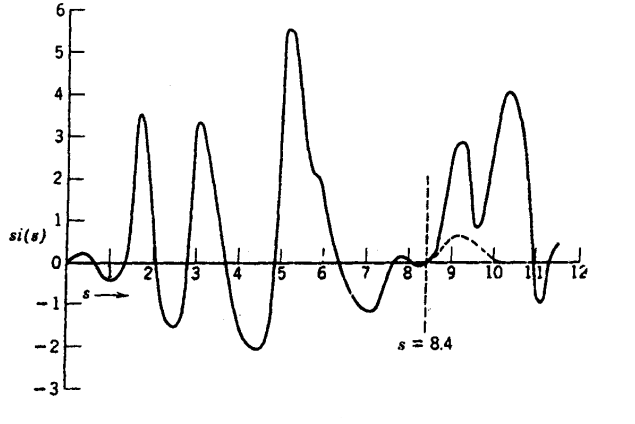
شكل (17-13)
دالة السعة العملية Si(s) لمادة الكربون
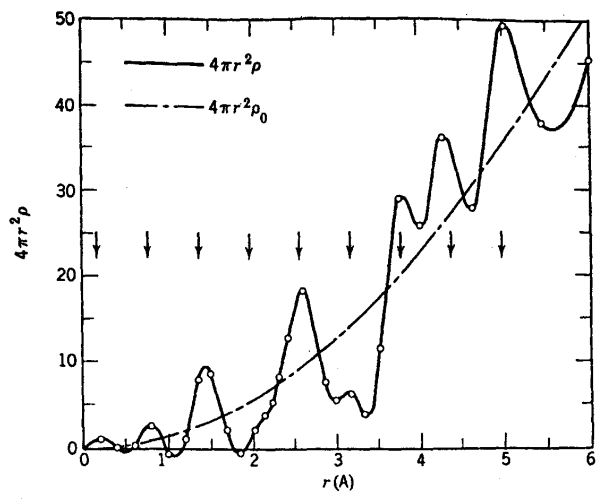
شكل (18-13)
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


