يستخدم الإشعاع السينكروتروني على نطاق واسع في علم البلورات الحديث، وفيما يلي نظرة عامة مختصرة عن هذه الأشعة وخواصها. إذا تحركت دقيقة مشحونة (إلكترون أو بوزيترون أو بروتون) بسرعة v في مجال مغناطيسي له مجال مغناطيسي تأثيري B في الاتجاه العمودي على المتجه B عندئذ تؤثر قوة على هذه الدقيقة قيمتها

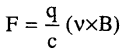
حيث q هي الشحنة للدقيقة بوحدات جاوس، c سرعة الضوء، ويكون اتجاه القوة F عموديا على كل من B، v وهذه القوة تولد عجلة جذب مركزية تجعل الدقيقة تتحرك على امتداد المحيط في مستوى عمودي على المتجه B.

وحسب قواعد الكهرومغناطيسية فإن الشحنة التي تتحرك على محيط يجب أن تشع طاقة كهرومغناطيسية على حساب طاقة الحركة المخزونة؛ ونتيجة لذلك يكون نصف قطر المسار (المدار) Trajectory هو:

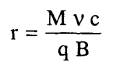
حيث M هي كتلة الدقيقة.

وبذلك تقل السرعة v للدقيقة، وتصبح حركة الدقيقة في المجال المغناطيسي تكون حلزونا مستويا يتقارب ليتجمع عند مركز المحيط.

وإذا زودت الدقيقة المشحونة بطاقة أثناء حركتها في المجال المغناطيسي، فإنه يمكن لها أن تعوض طاقة حركتها المفقودة في الإشعاع الكهرومغناطيسي، وذلك يجعل الدقيقة مجبرة على أن تبقى في مسار (trajectory) دائري، وفي مثل هذه الحالة تكون الدقيقة المشحونة التي تُعجل باستمرار بعجلة في المدى النسبي (relativistic) التي تتحرك في مجال مغناطيسي منتظم دائما مصدرا لأشعة كهرومغناطيسية تسمى أشعة سينكروترونية، والمعنى العريض لهذه التسمية سينكروترون هي المعجل الرنيني الدائري للدقائق المشحونة سواء الخفيف منها مثل الإلكترونات والبوزيترونات أو الثقيل منها مثل البروتونات والأيونات (شكل 1).

شكل (1)

شكل توضيحي لطريقة تعجيل الإلكترونات في المعجل (linac (lineal accelerator ثم بعد ذلك في المضخم Booster (لاحظ مقياس الرسم)

وطاقة الأشعة الكهرومغناطيسية التي تشع من دقيقة مشحونة متحركة في مدار دائري تعطى بالمعادلة:

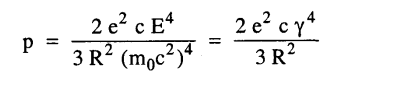
حيث p هي الطاقة المشعة في وحدة الزمن، e وهي شحنة الدقيقة، c سرعة الضوء، E هي طاقة الدقيقة، m₀ هي كتلتها في حالة السكون، R نصف قطر انحناء المسار (المدار)، وهذه المعادلة توضح السبب في أن الطاقة المشعة من الدقائق الثقيلة مثل البروتونات تكون منخفضة جدا والكمية γ وهي النسبة بين الطاقة الكلية والطاقة الساكنة تكون ذات أهمية؛ لأن العلاقة بينها وبين زاوية مخروط الأشعة تكون بالتقريب.

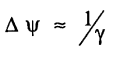
حيث Δψ هي زاوية الإشعاع بالتقدير الدائري.

وتكون الطاقة الكلية المنبعثة بواسطة الحلقة هي حاصل ضرب الطاقة المنبعثة من دقيقة أثناء دورة واحدة في عدد الدقائق ومقسوما على زمن الدورة الكاملة ويمكن إثبات أن الطاقة الكلية هي:

حيث تقاس طاقة الجزيئات بوحدات Ge V والمجال المغناطيسي B بوحدات التسلا، والتيار i بالأمبير والطاقة تعطى بوحدات kW؛ وبذلك نرى أن الطاقة تصبح متناسبة طرديا مع التيار في حلقة التخزين storage ring والخاصية الهامة للإشعاعات المولدة بواسطة المغناطيسيات المنحنية هو أن التوزيع الطيفي يكون متسع حيث يمكن توصيفه كميا بدلالة الفيض (Flux) الطيفي N وهو عدد الفوتونات التي تشع في وحدة الزمن في عرض شريطي قيمته λ/Δλ في زاوية dθ ويعطى بالمعادلة:

حيث يكون المعامل (Gi (y هو دالة تعتمد على الطاقة ويعرف المتغير y كالآتي:

y = h v/E_c

وتكون E_c هي الطاقة الحرجة المصاحبة لمجال مغناطيسي B الذي يعطى بالمعادلة:

E = 2.22 E³/R

حيث تقاس E بوحدات Ge V، R نصف قطر الانحناء المغناطيسي بالمتر ويمكن كتابة المعادلة السابقة كالآتي:

E = 0.665 E³ B

حيث تقاس B بوحدات التسلا Tesla.

والمتغير الشائع الاستعمال المعتمد على الطاقة الحرجة للفوتون هي طول الموجة الحرج _cλ شكل (2).

أي أن:

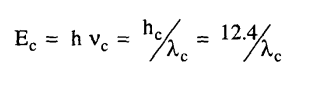
حيث تقاس E_c بوحدات keV، _cλ بالأنجستروم Å.

كما أنه من أهم خواص الإشعاع السينكروتروني الشدة العالية وشكل (3) يوضح العلاقة بين شدة الأشعة المولدة بواسطة سينكروترون إلكتروني وطول موجتها ويتضح كيف أن الأشعة السينكروترونية استثنائيا لها طيف متصل، وشدة الأشعة بطاقة قدرها GeV 5 تفوق الأشعة المولدة بالطريقة التقليدية بمقدار خمسة أو ستة أضعاف وتغير الشدة في المدى Å 2.5-0.5 يكون متواضع.

والخاصية الهامة الأخرى هو أن هذه الأشعة تكون مستقطبة لدرجة كبيرة فهي مستقطبة كليا في مستوى المدار ومستقطبة إلى حد كبير في الاتجاه العمودي ويوضح شكل (4) التوزيع الزاوي لشدة الأشعة السينكروترونية مع طول الموجة.

شكل (2)

التوزيع الطيفي لعدة حلقات تخزين لأجهزة مختلفة بالعالم

شكل (3)

اعتماد طاقة الاشعة السينكرونية على طول الموجة

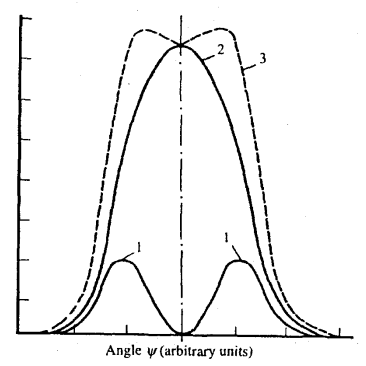
شكل (4)

التوزيع الزاوي لأشعة سينكرونية في الاتجاه العمودي 1 والاتجاه الموازي 2 حيث يكون 3 مجموعهما.

مواضيع ذات صلة

تأثير تصغير مقاييس الحبيبات على خواص المادة

الحبيبات

غياب المثالية عن الترتيب الذري

الشبكات البلورية

مراكز الالوان Color Centers

الأشعة وحيدة الموجة في تجارب الحيود من البلورات

شاشات عرض البلورات السائلة ذات المصفوفات الفعالة: «AMLCD «Active Matrix Liquid Crystal Display

استخدام البلورات السائلة في أجهزة العرض

السلوك الكهروبصري لأغشية (PDLC)

الخواص الكهروبصرية لأغشية البلورات السائلة المنتشرة داخل بوليمر «PDLC»

الانكسار المزدوج وتأثره بالمجال الكهربائي Birefringence

مواد بلورية سائلة جديدة