
NAND
 المؤلف:
Mendelson, E
المؤلف:
Mendelson, E
 المصدر:
Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.
المصدر:
Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 4-1-2022
4-1-2022
 1516
1516
NAND

NAND, also known as the Sheffer stroke, is a connective in logic equivalent to the composition NOT AND that yields true if any condition is false, and false if all conditions are true. 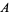 NAND
NAND 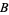 is equivalent to
is equivalent to 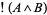 , where
, where 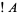 denotes NOT and
denotes NOT and 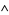 denotes AND. In propositional calculus, the term alternative denial is used to refer to the NAND connective. Notations for NAND include
denotes AND. In propositional calculus, the term alternative denial is used to refer to the NAND connective. Notations for NAND include 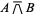 and
and 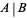 (Mendelson 1997, p. 26). The NAND operation is implemented as Nand[A, B, ...]. The circuit diagram symbol for an NAND gate is illustrated above.
(Mendelson 1997, p. 26). The NAND operation is implemented as Nand[A, B, ...]. The circuit diagram symbol for an NAND gate is illustrated above.
The binary NAND operator has the following truth table (Mendelson 1997, p. 27).
The NAND operation is the basic logical operation performed by the solid-state transistors ("NAND gates") that underlie virtually all integrated circuits and modern computers. The first axiom system based on NAND was given by Henry Sheffer in 1913. In their landmark tome, Whitehead and Russell (1927) promoted NAND as the appropriate foundation for axiomatic logic.
The AND function 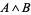 can be written in terms of NANDs as
can be written in terms of NANDs as
REFERENCES:
Mendelson, E. Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.
Simpson, R. E. "The NAND Gate." §12.5.5 in Introductory Electronics for Scientists and Engineers, 2nd ed. Boston, MA: Allyn and Bacon, pp. 548-550, 1987.
Whitehead, A. N. and Russell, B. Principia Mathematica. New York: Cambridge University Press, 1927.
 الاكثر قراءة في نظرية المجموعات
الاكثر قراءة في نظرية المجموعات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


