المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bitwin Chain |
 700
 04:09 مساءً
date: 5-9-2020 |
Author : Numbers. 
Book or Source : https://ourworld.compuserve.com/homepages/hlifchitz/Henri/us/NouvChPus.htm. 
Page and Part : ...|
Read More
Date: 23-11-2020
696
Date: 16-9-2020
714
Date: 30-11-2019
1170
|
A bitwin chain of length one consists of two pairs of twin primes with the property that they are related by being of the form:
 |
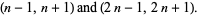(1) |
The first few values of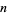 
generating bitwin chains are 6, 30, 660, 810, 2130, 2550, 3330, ... (OEIS A066388).
In general a chain of length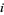 
consists of 
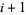pairs of twin primes,
 |
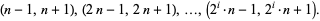(2) |
Bitwin chains can also be viewed as consisting of two related Cunningham chains of the first and second kinds,
 |
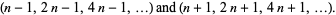(3) |
P. Jobling (1999) found the largest known chain of length six,
 |
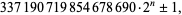(4) |
where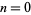 
to 6.
REFERENCES:
Jobling, P. "A BiTwin Chain of Length 6 Discovered." 4 Oct 1999. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9910&L=NMBRTHRY&P=151.
Lifchitz, H. "New Chains of Prime Numbers." https://ourworld.compuserve.com/homepages/hlifchitz/Henri/us/NouvChPus.htm.
Sloane, N. J. A. Sequence A066388 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|
