
Well-Defined
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-7-2018
25-7-2018
 2900
2900
Well-Defined
An expression is called "well-defined" (or "unambiguous") if its definition assigns it a unique interpretation or value. Otherwise, the expression is said to not be well-defined or to be ambiguous.
For example, the expression 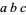 (the product) is well-defined if
(the product) is well-defined if 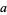 ,
, 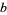 , and
, and 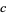 are integers. Because integers are associative,
are integers. Because integers are associative, 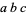 has the same value whether it is interpreted to mean
has the same value whether it is interpreted to mean 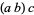 or
or 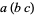 . However, if
. However, if 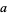 ,
, 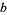 , and
, and 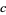 are Cayley numbers, then the expression
are Cayley numbers, then the expression 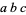 is not well-defined, since Cayley numbers are not, in general, associative, so that the two interpretations
is not well-defined, since Cayley numbers are not, in general, associative, so that the two interpretations 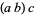 and
and 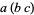 can be different.
can be different.
Sometimes, ambiguities are implicitly resolved by notational convention. For example, the conventional interpretation of 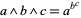 is
is 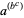 , never
, never 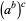 , so that the expression
, so that the expression 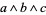 is well-defined even though exponentiation is nonassociative.
is well-defined even though exponentiation is nonassociative.
The term "well-defined" also has a technical meaning in field of partial differential equations. A solution to a partial differential equation that is a continuous function of its values on the boundary is said to be well-defined. Otherwise, a solution is called ill-defined.
 الاكثر قراءة في المعادلات التفاضلية الجزئية
الاكثر قراءة في المعادلات التفاضلية الجزئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


