A partial differential equation (PDE) is an equation involving functions and their partial derivatives; for example, the wave equation

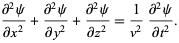(1)

Some partial differential equations can be solved exactly in the Wolfram Language using DSolve[eqn, y, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline1.gif" style="height:14px; width:5px" />x1, x2}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline2.gif" style="height:14px; width:5px" />], and numerically using NDSolve[eqns, y, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline3.gif" style="height:14px; width:5px" />x, xmin, xmax}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline4.gif" style="height:14px; width:5px" />, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline5.gif" style="height:14px; width:5px" />t, tmin, tmax}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline6.gif" style="height:14px; width:5px" />].

In general, partial differential equations are much more difficult to solve analytically than are ordinary differential equations. They may sometimes be solved using a Bäcklund transformation, characteristics, Green's function, integral transform, Lax pair, separation of variables, or--when all else fails (which it frequently does)--numerical methods such as finite differences.

Fortunately, partial differential equations of second-order are often amenable to analytical solution. Such PDEs are of the form

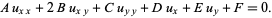(2)

Linear second-order PDEs are then classified according to the properties of the matrix

(3)

as elliptic, hyperbolic, or parabolic.

If 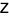 is a positive definite matrix, i.e., 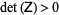, the PDE is said to be elliptic. Laplace's equation and Poisson's equation are examples. Boundary conditions are used to give the constraint  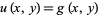on 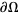, where

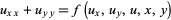(4)

holds in .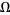

If det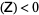, the PDE is said to be hyperbolic. The wave equation is an example of a hyperbolic partial differential equation. Initial-boundary conditions are used to give

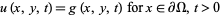(5)

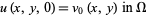(6)

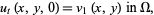(7)

where

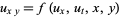(8)

holds in .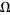

If det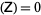, the PDE is said to be parabolic. The heat conduction equation equation and other diffusion equations are examples. Initial-boundary conditions are used to give

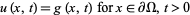(9)

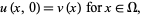(10)

where

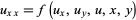(11)

holds in .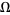

The following are examples of important partial differential equations that commonly arise in problems of mathematical physics.

Benjamin-Bona-Mahony equation

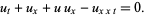(12)

Biharmonic equation

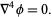(13)

Boussinesq equation

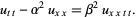(14)

Cauchy-Riemann equations

			(15)
			(16)

Chaplygin's equation

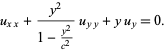(17)

Euler-Darboux equation

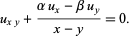(18)

Heat conduction equation

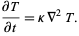(19)

Helmholtz differential equation

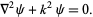(20)

Klein-Gordon equation

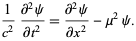(21)

Korteweg-de Vries-Burgers equation

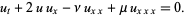(22)

Korteweg-de Vries equation

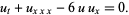(23)

Krichever-Novikov equation

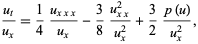(24)

where

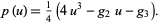(25)

Laplace's equation

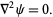(26)

Lin-Tsien equation

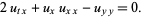(27)

Sine-Gordon equation

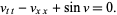(28)

Spherical harmonic differential equation

(29)

Tricomi equation

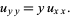(30)

Wave equation

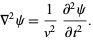(31)

REFERENCES:

Arfken, G. "Partial Differential Equations of Theoretical Physics." §8.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 437-440, 1985.

Bateman, H. Partial Differential Equations of Mathematical Physics. New York: Dover, 1944.

Conte, R. "Exact Solutions of Nonlinear Partial Differential Equations by Singularity Analysis." 13 Sep 2000. http://arxiv.org/abs/nlin.SI/0009024.

Kamke, E. Differentialgleichungen Lösungsmethoden und Lösungen, Bd. 2: Partielle Differentialgleichungen ester Ordnung für eine gesuchte Function. New York: Chelsea, 1974.

Folland, G. B. Introduction to Partial Differential Equations, 2nd ed. Princeton, NJ: Princeton University Press, 1996.

Kevorkian, J. Partial Differential Equations: Analytical Solution Techniques, 2nd ed. New York: Springer-Verlag, 2000.

Morse, P. M. and Feshbach, H. "Standard Forms for Some of the Partial Differential Equations of Theoretical Physics." Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 271-272, 1953.

Polyanin, A.; Zaitsev, V.; and Moussiaux, A. Handbook of First-Order Partial Differential Equations. New York: Gordon and Breach, 2001.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Partial Differential Equations." Ch. 19 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 818-880, 1992.

Sobolev, S. L. Partial Differential Equations of Mathematical Physics. New York: Dover, 1989.

Sommerfeld, A. Partial Differential Equations in Physics. New York: Academic Press, 1964.

Taylor, M. E. Partial Differential Equations, Vol. 1: Basic Theory. New York: Springer-Verlag, 1996.

Taylor, M. E. Partial Differential Equations, Vol. 2: Qualitative Studies of Linear Equations. New York: Springer-Verlag, 1996.

Taylor, M. E. Partial Differential Equations, Vol. 3: Nonlinear Equations. New York: Springer-Verlag, 1996.

Trott, M. "The Mathematica Guidebooks Additional Material: Various Time-Dependent PDEs." http://www.mathematicaguidebooks.org/additions.shtml#N_1_06.

Webster, A. G. Partial Differential Equations of Mathematical Physics, 2nd corr. ed. New York: Dover, 1955.

Weisstein, E. W. "Books about Partial Differential Equations." http://www.ericweisstein.com/encyclopedias/books/PartialDifferentialEquations.html.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.