A partial differential equation (PDE) is an equation involving functions and their partial derivatives; for example, the wave equation

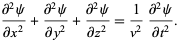(1)

Some partial differential equations can be solved exactly in the Wolfram Language using DSolve[eqn, y, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline1.gif" style="height:14px; width:5px" />x1, x2}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline2.gif" style="height:14px; width:5px" />], and numerically using NDSolve[eqns, y, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline3.gif" style="height:14px; width:5px" />x, xmin, xmax}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline4.gif" style="height:14px; width:5px" />, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline5.gif" style="height:14px; width:5px" />t, tmin, tmax}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline6.gif" style="height:14px; width:5px" />].

In general, partial differential equations are much more difficult to solve analytically than are ordinary differential equations. They may sometimes be solved using a Bäcklund transformation, characteristics, Green's function, integral transform, Lax pair, separation of variables, or--when all else fails (which it frequently does)--numerical methods such as finite differences.

Fortunately, partial differential equations of second-order are often amenable to analytical solution. Such PDEs are of the form

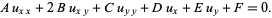(2)

Linear second-order PDEs are then classified according to the properties of the matrix

(3)

as elliptic, hyperbolic, or parabolic.

If 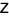 is a positive definite matrix, i.e., 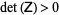, the PDE is said to be elliptic. Laplace's equation and Poisson's equation are examples. Boundary conditions are used to give the constraint  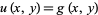on 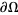, where

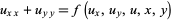(4)

holds in .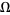

If det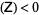, the PDE is said to be hyperbolic. The wave equation is an example of a hyperbolic partial differential equation. Initial-boundary conditions are used to give

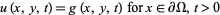(5)

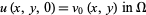(6)

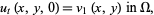(7)

where

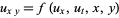(8)

holds in .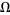

If det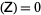, the PDE is said to be parabolic. The heat conduction equation equation and other diffusion equations are examples. Initial-boundary conditions are used to give

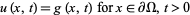(9)

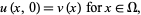(10)

where

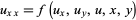(11)

holds in .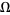

The following are examples of important partial differential equations that commonly arise in problems of mathematical physics.

Benjamin-Bona-Mahony equation

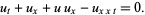(12)

Biharmonic equation

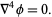(13)

Boussinesq equation

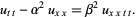(14)

Cauchy-Riemann equations

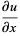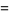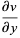			(15)
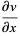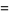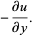			(16)

Chaplygin's equation

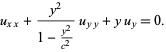(17)

Euler-Darboux equation

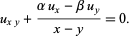(18)

Heat conduction equation

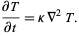(19)

Helmholtz differential equation

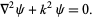(20)

Klein-Gordon equation

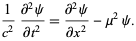(21)

Korteweg-de Vries-Burgers equation

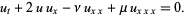(22)

Korteweg-de Vries equation

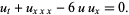(23)

Krichever-Novikov equation

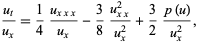(24)

where

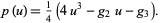(25)

Laplace's equation

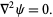(26)

Lin-Tsien equation

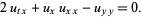(27)

Sine-Gordon equation

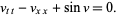(28)

Spherical harmonic differential equation

(29)

Tricomi equation

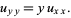(30)

Wave equation

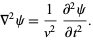(31)

REFERENCES:

Arfken, G. "Partial Differential Equations of Theoretical Physics." §8.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 437-440, 1985.

Bateman, H. Partial Differential Equations of Mathematical Physics. New York: Dover, 1944.

Conte, R. "Exact Solutions of Nonlinear Partial Differential Equations by Singularity Analysis." 13 Sep 2000. http://arxiv.org/abs/nlin.SI/0009024.

Kamke, E. Differentialgleichungen Lösungsmethoden und Lösungen, Bd. 2: Partielle Differentialgleichungen ester Ordnung für eine gesuchte Function. New York: Chelsea, 1974.

Folland, G. B. Introduction to Partial Differential Equations, 2nd ed. Princeton, NJ: Princeton University Press, 1996.

Kevorkian, J. Partial Differential Equations: Analytical Solution Techniques, 2nd ed. New York: Springer-Verlag, 2000.

Morse, P. M. and Feshbach, H. "Standard Forms for Some of the Partial Differential Equations of Theoretical Physics." Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 271-272, 1953.

Polyanin, A.; Zaitsev, V.; and Moussiaux, A. Handbook of First-Order Partial Differential Equations. New York: Gordon and Breach, 2001.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Partial Differential Equations." Ch. 19 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 818-880, 1992.

Sobolev, S. L. Partial Differential Equations of Mathematical Physics. New York: Dover, 1989.

Sommerfeld, A. Partial Differential Equations in Physics. New York: Academic Press, 1964.

Taylor, M. E. Partial Differential Equations, Vol. 1: Basic Theory. New York: Springer-Verlag, 1996.

Taylor, M. E. Partial Differential Equations, Vol. 2: Qualitative Studies of Linear Equations. New York: Springer-Verlag, 1996.

Taylor, M. E. Partial Differential Equations, Vol. 3: Nonlinear Equations. New York: Springer-Verlag, 1996.

Trott, M. "The Mathematica Guidebooks Additional Material: Various Time-Dependent PDEs." http://www.mathematicaguidebooks.org/additions.shtml#N_1_06.

Webster, A. G. Partial Differential Equations of Mathematical Physics, 2nd corr. ed. New York: Dover, 1955.

Weisstein, E. W. "Books about Partial Differential Equations." http://www.ericweisstein.com/encyclopedias/books/PartialDifferentialEquations.html.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم التطوير يقيم دورة عن أخلاقيات المهنة للمنتسبين الجدد

تتضمن زيارة المراقد المقدسة في كربلاء.. معهد القرآن الكريم النسوي ينظم سفرة دينية لطالباته

المجمع العلمي يحتفي بذكرى ولادة الإمامين الباقر والهادي (عليهما السلام)

قسم الشؤون الفكرية يطلق فعاليات الأسبوع الثالث من برنامج البذرة الصالحة

المزيد

الآخبار الصحية

ثورة طبية.. الذكاء الاصطناعي يكشف سرطان الكلى في وقت قياسي

لتعزيز الطاقة والتغلب على التعب.. عليك بـ7 طرق بسيطة

لتحسين الهضم والتحكم في الشهية.. ما أفضل وقت لتناول التمر؟

خبراء يكشفون تأثير الاستحمام في الظلام على جودة النوم !

المزيد

الآخبار التكنلوجية

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

نظائر الهيليوم مقياس لاكتشاف رواسب الذهب.. كيف ذلك؟

الصين تطلق أول ناقلة نفط خام ذكية في العالم تعمل بالميثانول

الزمن على المريخ أسرع من الأرض.. دراسة علمية تكشف الفوارق

المزيد