Laplace Equation--Confocal Ellipsoidal Coordinates

Using the notation of Byerly (1959, pp. 252-253), Laplace's equation can be reduced to

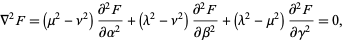(1)

where

			(2)
			(3)
			(4)
			(5)
			(6)
			(7)

In terms of 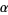, , 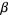and ,

			(8)
			(9)
			(10)

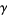Equation (◇) is not separable using a function of the form

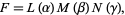(11)

but it is if we let

			(12)
			(13)
			(14)

These give

			(15)
			(16)

and all others terms vanish. Therefore (◇) can be broken up into the equations

			(17)
			(18)
			(19)

For future convenience, now write

			(20)
			(21)

then

			(22)
			(23)
			(24)

Now replace 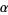, , 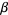and 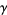 to obtain

(25)

Each of these is a Lamé's differential equation, whose solution is called an ellipsoidal harmonic of the first kind. Writing

			(26)
			(27)
			(28)

gives the solution to (◇) as a product of ellipsoidal harmonics of the first kind .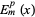

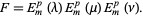(29)

REFERENCES:

Arfken, G. "Confocal Ellipsoidal Coordinates ." §2.15 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 251-258, 1959.

Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 43-44, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.