Radian and degree measures of angles

Degree and radian measures of angles. 
Relation of a circle radius and a circumference 
length. Table of degree and radian measures 
for some most used angles.

A degree measure. Here a unit of measurement is a degree (its designation is ° or  deg ) – a turn of a ray by the  1 / 360   part of the one complete revolution. So, the complete revolution of a ray is equal to 360 deg. One degree is divided into 60 minutes (a designation is ‘ or  min); one minute – correspondingly into  60 seconds (a designation is “ or  sec).

A radian measure. As we know from plane geometry ( see the point "A length of arc" of the paragraph "Geometric locus. Circle and circumference"), a length of an arc l , a radius  r and a corresponding central angle α are tied by the relation:

α = l / r .

This formula is a base for definition of a radian measure of angles. So,  if  l = r , then α = 1, and we say, that an angle  α is equal to1 radian, that is designed as α = 1 rad.  Thus, we have the following definition of a radian measure unit:

A radian is a central angle, for which lengths of  its arc and radius are equal ( AmB = AO, Fig.1 ). So, a radian measure of any angle is a ratio of a length of an arc drawn by an arbitrary radius and concluded between sides of this angle to the arc radius.

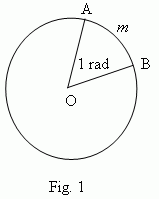
Following this formula, a length of a circumference  C   and its radius  r  can be expressed as:

2 α =  C / r .

So, a round angle, equal to 360° in a degree measure, is simultaneously  2α in a radian measure. Hence, we receive a value of one radian:

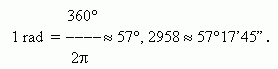
Inversely,

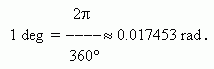
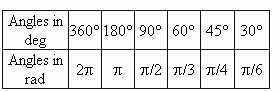
It is useful to remember the following comparative table of degree and radian measure for some angles, we often deal with:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الطبية يقدم الخدمات الصحية والعلاجية لزائري مدينة سامراء

العتبة العباسية المقدسة تقدم خدماتها لزائري مرقد الإمامين العسكريين (عليهما السلام) في سامراء

المجمَع العلمي ووفد وزارة التربية يبحثان سبل التعاون المشترك

قسم الشؤون الفكرية يصدر العدد 192 من مجلة الرياحين للأطفال

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد

مواضيع ذات صلة

Trigonometric inequalities

Trigonometric functions of any angle

Trigonometric functions of an acute angle

Trigonometric equations. Main methods for solving

Transforming of trigonometric expressions to product

Transforming of degree measure to radian one and back

Systems of simultaneous trigonometric equations

Some important correlations

Solving of right-angled triangles

Relations between trigonometric functions of the same angle

Reduction formulas

Problems: Trigonometric transformations