Conservation of Linear Momentum
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 116
28-12-2016
2619
Conservation of Linear Momentum
If all the external forces are zero (Σ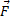
ext = 0) then 
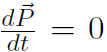which implies that the total momentum
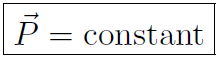(1.1)
Note that this is only true if all the external forces are zero. Halliday calls this a closed, isolated system. Another way of stating (1.1) is
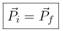
Remembering that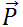 
is the total momentum of a system of particles (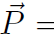
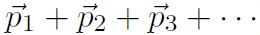), the conservation equation is
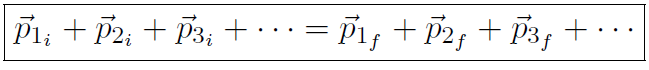
This is a vector equation, so we must always write it out in x, y, or z components.
Example A rifle of mass mR fires a bullet of mass mB which emerges at a speed of vBf . With what speed does the rifle recoil ?
Solution The bullet-rifle system is a closed, isolated system. When the rifle is held at rest the sum of all external forces is zero. Thus momentum is conserved for the bullet (B)-rifle (R) two body system. The total momentum is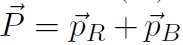 
, so that conservation of momentum is
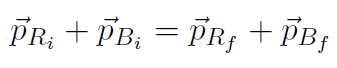
Now this is a vector equation, so it must be written in terms of components, namely
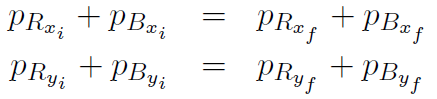
but there is only motion in the x direction and nothing is happening in the y direction, so let's re-write the x-equation, leaving off the x's as
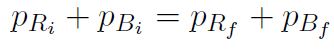
or
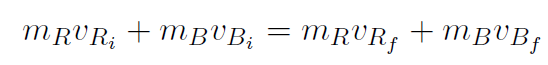
But vRi + vBi = 0 because before the gun is fired (initial situation) the bullet and gun do not move. After the gun is fired (final situation) they both move. Thus
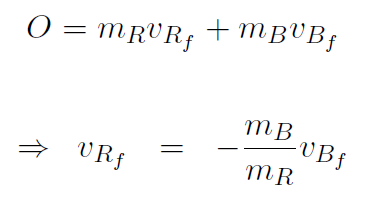
where the minus sign indicates that the rifle moves in a direction opposite to the bullet.
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
