Shallow Square Well II

A particle of mass m is confined to move in one dimension by a potential V(x) (see Figure 1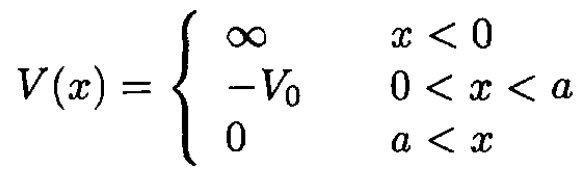.1):

(1)

Figure 1.1

a) Derive the equation for the bound state.

b) From the results of part (a), derive an expression for the minimum value of V₀ which will have a bound state.

c) Give the expression for the eigenfunction of a state with positive energy E > 0.

d) Show that the results of (c) define a phase shift for the potential, and derive an expression for the phase shift.

SOLUTION

a) For the bound state we can write the eigenvalue as E = -h²α²/2m, where α is the decay constant of the eigenfunction outside the square well. Inside the square well we define a wave vector k by

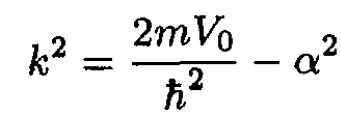(1)

The infinite potential at the origin requires that all eigenfunctions vanish at x = 0. So the lowest eigenfunction must have the form

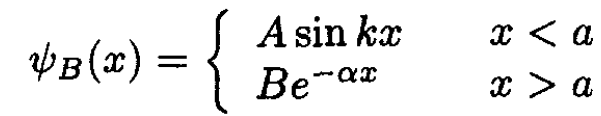(2)

At the point x = a, we match the eigenfunctions and their derivatives:

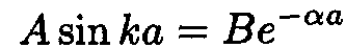(3)

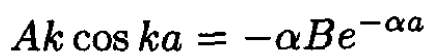(4)

We eliminate the constants A and B by dividing these two equations:

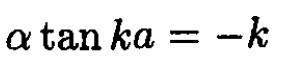(5)

Earlier we established the relationship between k and α. So the only unknown variable is α, which is determined by this equation.

b) To find the minimum bound state, we take the limit α → 0 as in the eigenvalue equation. From (1) we see that k goes to a nonzero constant, and the eigenvalue equation only makes sense as α → 0  if tan ka → ∞, which happens at ka → π/2.  Using (1) gives π²/4 = k²a² = 2mV₀a²/h². Thus, we derive the minimum value of V₀ for a bound state:

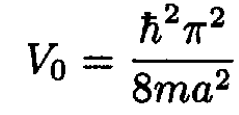(6)

c) For a positive energy state set 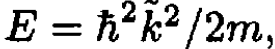 where  is the wave vector outside the square well. Inside the square well we again define a wave vector k according to

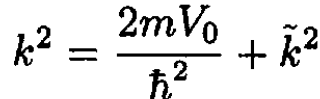(7)

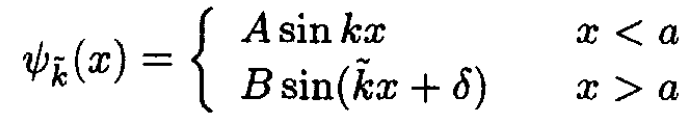(8)

Again we have the requirement that the eigenfunction vanish at x = 0. For x > a we have an eigenfunction with two unknown parameters B and δ. Alternatively, we may write it as

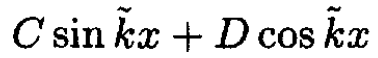(9)

in terms of two unknowns C and D. The two forms are equivalent since C = B cos δ, D = B sin δ. We prefer to write it with the phase shift δ. Again we match the two wave functions and their derivatives at x = a:

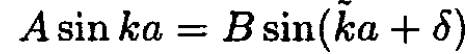(10)

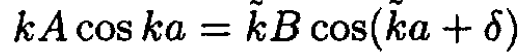(11)

Dividing (10) by (11), we obtain

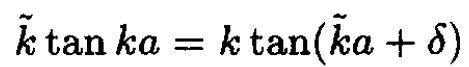(12)

Since k is a known function of  the only unknown in this equation is δ, which is determined by this equation.

d) From (12) we derive an expression for the phase shift:

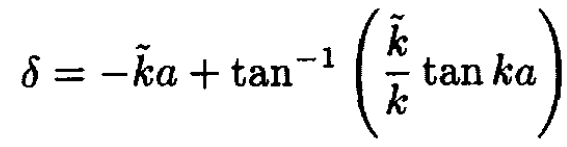(13)

اخر الاخبار

اخبار العتبة العباسية المقدسة

خدمات فكرية وثقافية عديدة قدمها مركز مُلتقى القمر الثقافي لزائري الأربعين

إحياءً لذكرى زيارة الأربعين.. العتبة العباسية المقدسة تواصل إقامة مجلسها العزائي

عبر كاميرات تعمل بالذكاء الاصطناعي.. قسم الاتصالات يوضح تفاصيل جديدة حول آلية عدِّ زائري الأربعين

شعبة الخطابة الحسينية النسوية تواصل نشاطاتها الفكرية والثقافية في مجمع الشيخ الكليني

المزيد

الآخبار الصحية

حجم جزء محدد من الجسم يعكس الصحة العامة ومخاطر الأمراض

تفشي عدوى بكتيرية بفرنسا يحتمل ارتباطها بنوع من الجبن الطري

دراسة حديثة تكشف ما تفعله الشاشات بـ"قلوب الأطفال" !

متلازمة المبنى المريض.. هكذا يتحول تكييف الهواء إلى خطر صحي ؟؟

المزيد

الآخبار التكنلوجية

كيف تتعامل مع حرارة الطقس أثناء القيادة؟

لماذا يجب عليك إيقاف تكييف السيارة قبل إطفاء المحرك؟

دراسة تكشف سببا محتملا وراء زيادة خطر إصابة الأطفال بالتوحد

تشيلي.. العثور على متحجرة حيوان ثديي صغير من زمن الديناصورات

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين