Retarded Potential of Moving Line Charge
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 70
11-8-2016
2004
Retarded Potential of Moving Line Charge
An infinitely long insulating filament with linear charge density λ lies at rest along the z-axis (see Figure 1.1).
a) Find the electrostatic field Er at a point P a distance x0 away from the origin along the x-axis.
b) At t = 0 the wire suddenly starts to move with constant velocity v in the positive direction. Assuming the wire is infinitely thin, write down an expression for the current density J arising from the motion. Using the formula for the retarded potential
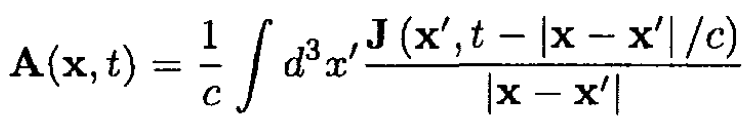
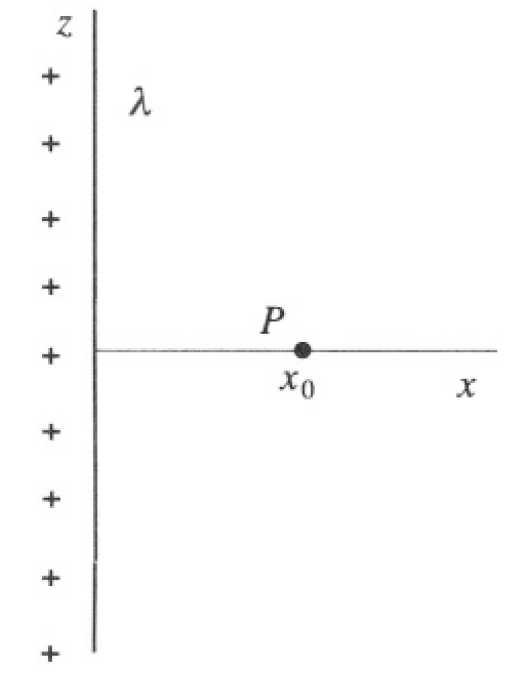
Figure 1.1
Calculate Az (x0, t) Give its value for t > x0/c and for t < x0/c.
c) Because of cylindrical symmetry, you really know Az (ρ, t) with ρ the radial coordinate in cylindrical coordinates. Find B (ρ, t) as t →∞. Does your value agree with your intuitive expectation from Ampere’s law?
Hint: A useful integral is
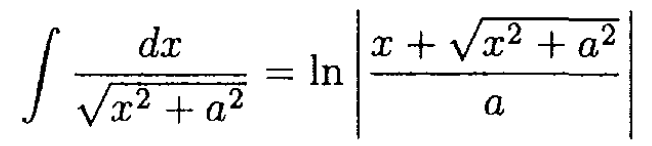
SOLUTION
a) We may calculate the field of a line charge using Gauss’s law
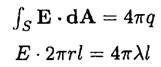
where r is the distance from the line charge and is some length of wire. So
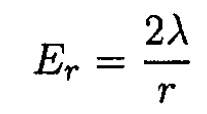(1)
b) The current density
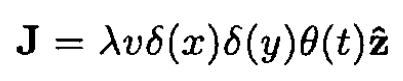(2)
where δ is the Dirac delta function and θ (t) is defined by
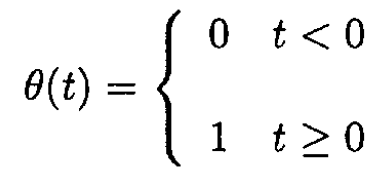
We may then write
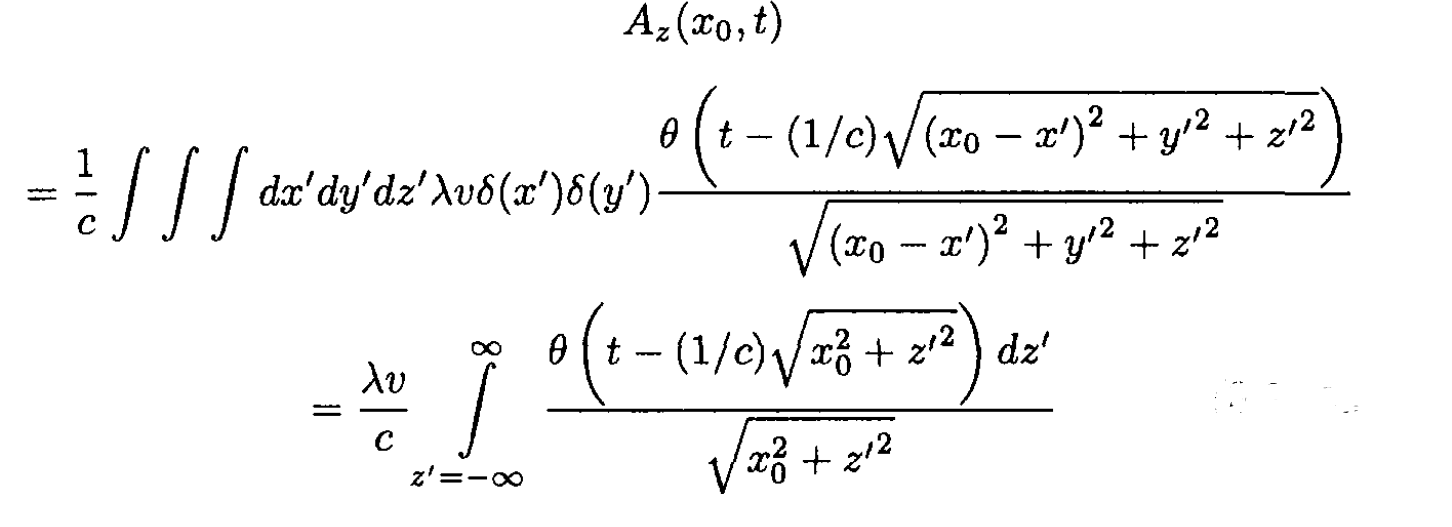(3)
Now,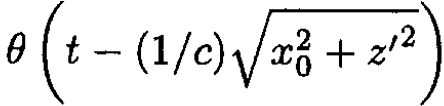 
is zero unless
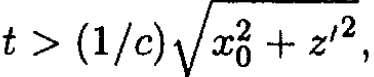so
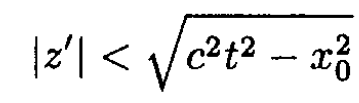
and the integral in (3) becomes
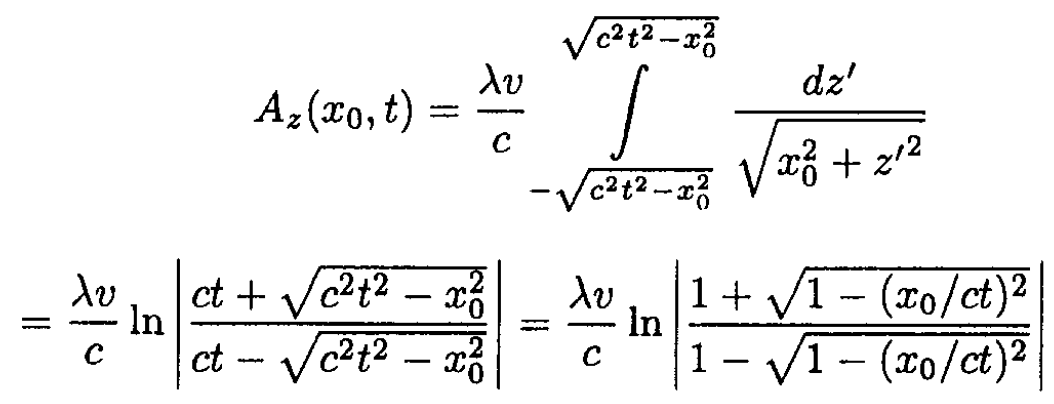(4)
for t > x0/c. For t < x0/c, Az (x0, t) = 0.
c) From (4), we have for ρ < ct.
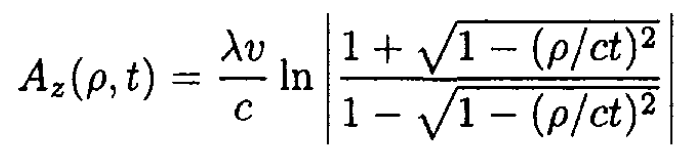(5)
By definition, 
which in cylindrical coordinates gives
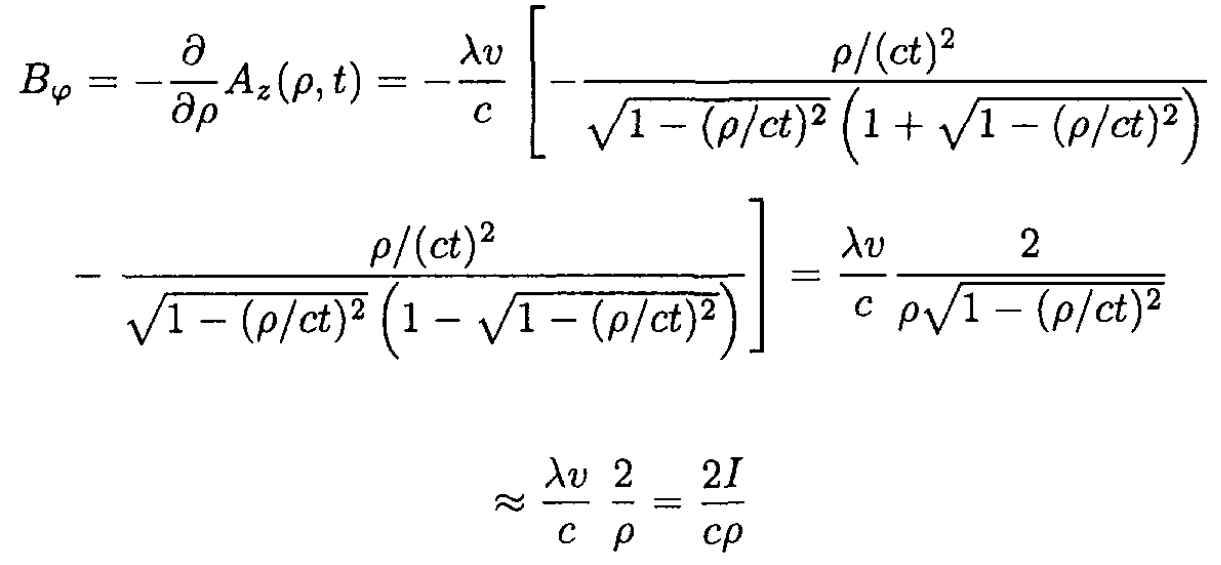
for t → ∞, which is the value of the magnetic field that would result from a calculation using Ampere’s law.
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
