Electrons and Circularly Polarized Waves
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 67
9-8-2016
1598
Electrons and Circularly Polarized Waves
a) An electron (mass m, charge -e ) is subject to the elastic force F = -m ω20r. A static, uniform magnetic field B in the positive z direction is also present. The electron is set in forced motion by one of the circularly polarized electromagnetic waves
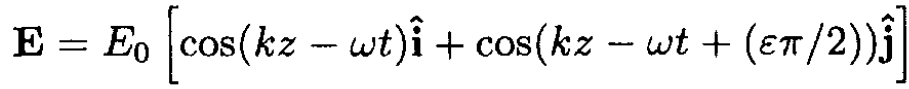
(ε = -1 positive helicity, ε = 1 negative helicity). Find the coordinates of the electron as functions of time.
Hints: Approximate E by its value for z = 0. The use of the variables ζ = x + iy and η = x - iy will simplify your calculations.
b) Consider circularly polarized electromagnetic waves propagating in the direction of a static magnetic field B in a medium consisting of elastically bound electrons (N per unit volume). The elementary theory of dispersion leads to the formula
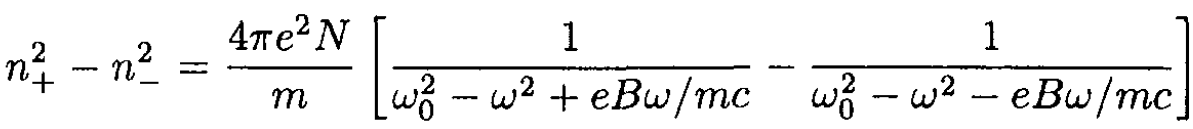
for the refractive indices (n+, n-) of circularly polarized waves of (positive, negative) helicity.
Without proving this formula, infer from it that the plane of polarization of a linearly polarized wave is rotated through the angle
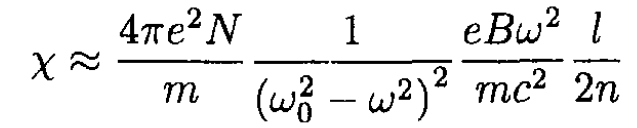(i)
after propagating through a length in the medium when a magnetic field in the direction of propagation is present.
Hint: Represent a linearly polarized wave as a sum of circularly polarized waves of opposite helicities.
SOLUTION
a) Find the equations of motion of the electron in the x and y directions at z = 0 for ε = -1:
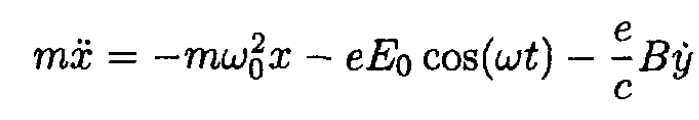(1)
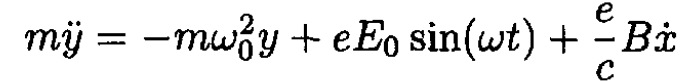(2)
Multiply (2) by -i and add to (1). Substituting the variable η from the hint in the problem, we obtain
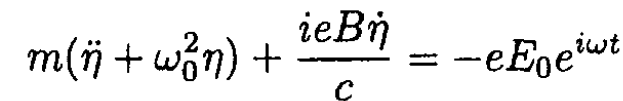(3)
(3) may be solved by finding a solution at the driving frequency ω:
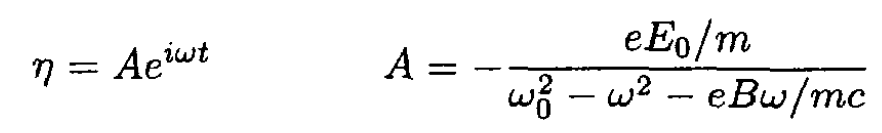
The analogous differential equation for is formed by multiplying (2) by and adding to (1). We find that ζ = A exp (-iωt). This gives for the original variables
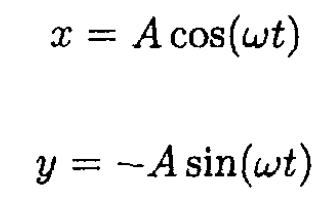
For ε = +1, we have
where
Here,
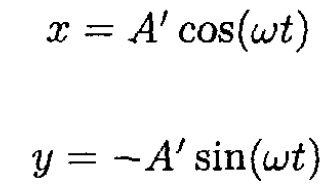
b) A linearly polarized wave may be viewed as the sum of two circularly polarized waves of opposite helicity (see Figure 1.1). After propagating through the medium, the waves will be delayed by different phases, given
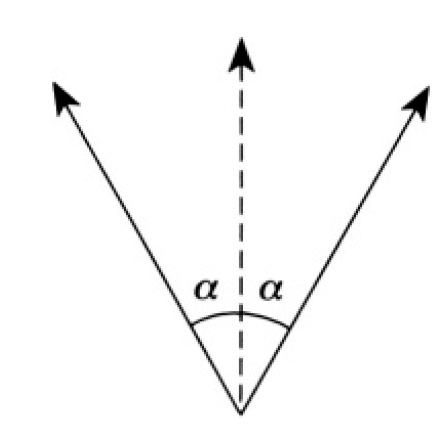
Figure 1.1
by a+ and a-
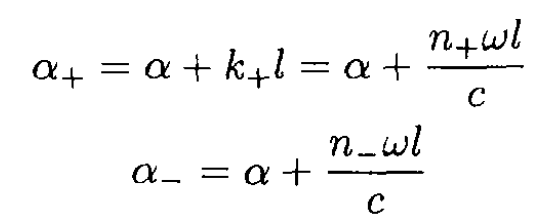
The plane of polarization is now along the bisector of the circularly polarized vectors and forms with the initial plane of polarization the angle
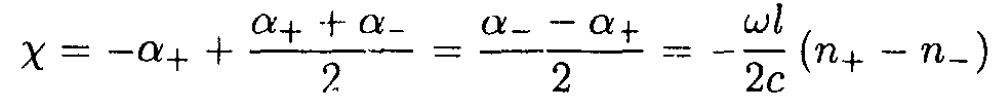(4)
(5)
where 2n ≈ n+ + n-. Substituting (i) into (5), we obtain
(6)
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
