Linear codes are necessarily fixed-length. Many codes are like this, but some codes use different length words.

One well-known example is the Morse code. It was designed for sending Englishlanguage messages by telegraph, and it was desirable to make the transmissions as short as possible. For this reason, those letters that occur most commonly in English have shorter representations.

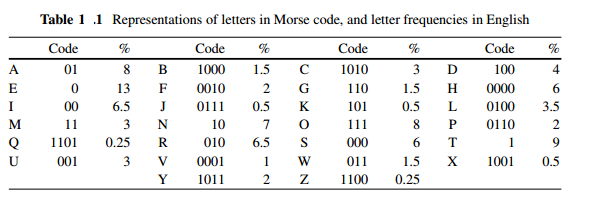
The Morse code is binary. The two symbols are the dot and the dash, where the dot is a short transmission and the dash is a longer one, as long as three dots. Each dot or dash is followed by a short silence, equal to the dot duration; the letters of a word are separated by a silence equal to three dots (one dash), and two words are separated by a space equal to seven dots. For convenience, we shall represent the dot by 0 and the dash by 1. Table 1.1 shows the Morse code for letters, and also the approximate frequency of letters in English. Table 1.2 shows how numbers are represented in the code.

Sample Problem 1.1 How is the phrase “bring food” represented in Morse code?

Solution. 1000 010 00 10 110 0010 111 111 100

The Morse code is an example of a variable-length code. Some variable-length codes use a break to symbolize the end of a word, either a physical break in transmission (like the Morse code) or an “end-of-line” symbol; in others, the codewords can include information that signals the end of the word. For example, if every codeword ends in 00, and there are never two consecutive 0s in a word, each 00 would tell you when a word ends.

Another important example is the genetic code. Genes are built from four nucleotides: adenine, thymine, Guanine, and cytosine. A gene can be specified by a sequence of these, usually represented by the initials A, T, G, and C.

Suppose we want to use a binary code to represent a genetic string. One possibility is to use the codewords 00 for A, 01 for C, 10 for G, and 11 for T.

For example, AACAGTAAAC would be represented by 00000100101100000001  (20 symbols).

It happens that A is most common in genetic strings, then C, then T and G. We could try the following encoding:

0 for A, 10 for C, 110 for T, 111 for G.

Then AACAGTAAAC is represented by 0010011111000010 (16 symbols). We shall call this the genetic code. Notice that, in the suggested encoding method, every time 111 occurs, it is the codeword for G, and every time a 0 occurs, it is at the end of a codeword. Moreover, the only way a codeword can end is with 0 or 111. So here is a technique for decoding the genetic code. First, put commas after each occurrence of 0 or 111. Then decode the strings between the commas. For example, the string

001100101110110110000010

is written

0,0,110,0,10,111,0,110,110,0,0,0,0,10

which decodes to

AATACGATTAAAAC.

مواضيع ذات صلة

Remez Algorithm

Quadratic Phase Array

Fractional Fourier Transform

Circulant Matrix

Logistic Map--r=-2

Logistic Map--r=2

Logistic Map--r=4

Lotka-Volterra Equations

Population Growth

Survivorship Curve

Tent Map

Traveling Salesman Problem