الحركة الخطية بتسارع منتظم

(One Dimensional Motion With Uniform Acceleration)

تعتبر حركة الأجسام بتسارع منتظم من ابسط انواع الحركة الخطية والتي عددها يكون معدل تسارع الجسم مساوياً للتسارع الآني 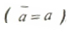. ومن اجل تبسيط وضع المعادلات الخاصة بهذا النوع من الحروف سوف نستخدم مجموعة من الافتراضات والرموز وكما يلي:

نفترض أن زمن بداية الحركة للجسم يساوي صفراً، (0 = t_i).

وإن زمن نهاية الحركة يساوي ، (t = t_f). 

وإن السرعة البدائية للجسم تساوي ، (v_i = v₀).

وإن السرعة النهائية للجسم تساوي  ، (v_f = v).

وهكذا يمكن وضع معادلة التسارع كما يلي:

وبذلك فإن: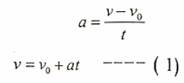               

وهذه العلاقة تمثل اولى علاقات الحركة الخطية (Kinematics equation) بين سرعة الجسم والتسارع والزمن والتي يمكن تمثيلها في الشكل رقم (1-1) الذي يبين العلاقة بين سرعة الجسم والزمن حيث يلاحظ ان الجسم عند الزمن 0 = t فإن الجس سوف يمتلك سرعة اولية مقدارها V₀، وبعد مرور فترة من الزمن فإن سرعة الجسم سوف تزداد بمقدار حاصل ضرب التسارع في الزمن كما في المعادلة السابقة التي تمثل معادلة خط مستقيم ميله يساوي (a) ومقطعه على المحور الصادي يمثل (V₀).

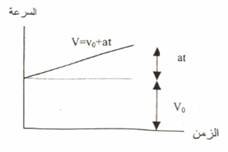
الشكل (1.1)

وعند تباطأ سرعة الجسم، بعد مرور فترة من الزمن مقدارها (t)، فإن تسارع الجسم سوف يكون سالباً حيث (v = v₀ – at)، ويمكن رسم دالة السرعة بالنسبة للزمن عندئذ كما في الشكل (1.2) حيث ميل المستقيم يمثل التسارع (-a) (سالب الإشارة)، وأن المقطع على المحور الصادي يمثل V₀ حيث عند الزمن 0 = t كون v₀ مساوية إلى v.

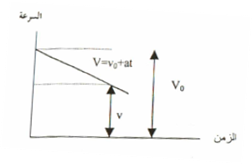
الشكل (1.2)

وكذلك يمكن وضع معادلة معدل السرعة عند ثبات التسارع كما يلي:

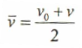
فإذا رمزنا الإحداثي الموقع الأول للجسم بــ X₀ ولإحداثي الموقع النهائي للجسم بــ x يمكن وضع معادلة سرعة الجسم كما يلي:

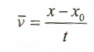
وبذلك فأن:

وبتبسيط المعادلة نحصل على:

          (2) 

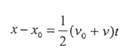
وتمثل هذه العلاقة القانون الثاني من قوانين الحركة الخطية .

وبتعويض قيمة السرعة v من المعادلة الاولى في المعادلة الثانية نحصل على:

ومنه نحصل على القانون الثالث من قوانين الحركة الخطية:

(3)   

ويلاحظ من المعادلات (3 , 2 , 1) ان جميعها تحتوي على عامل الزمن، ولجل وضع قانون آخر لا يحتوي على عامل الزمن تعويض الزمن من المعادلة (1) في المعادلة (2) فنحصل على:

وبتبسيط الحدود نحصل على القانون الرابع ممن قوانين الحركة الخطية العلاقة:

(4)    

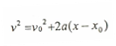
ويمكننا تلخيص قوانين الحركة الخطية في الجدول رقم (1.1) لسهولة الرجوع

الجدول (1.1)

اخر الاخبار

اخبار العتبة العباسية المقدسة

خدمات فكرية وثقافية عديدة قدمها مركز مُلتقى القمر الثقافي لزائري الأربعين

إحياءً لذكرى زيارة الأربعين.. العتبة العباسية المقدسة تواصل إقامة مجلسها العزائي

عبر كاميرات تعمل بالذكاء الاصطناعي.. قسم الاتصالات يوضح تفاصيل جديدة حول آلية عدِّ زائري الأربعين

شعبة الخطابة الحسينية النسوية تواصل نشاطاتها الفكرية والثقافية في مجمع الشيخ الكليني

المزيد

الآخبار الصحية

حجم جزء محدد من الجسم يعكس الصحة العامة ومخاطر الأمراض

تفشي عدوى بكتيرية بفرنسا يحتمل ارتباطها بنوع من الجبن الطري

دراسة حديثة تكشف ما تفعله الشاشات بـ"قلوب الأطفال" !

متلازمة المبنى المريض.. هكذا يتحول تكييف الهواء إلى خطر صحي ؟؟

المزيد

الآخبار التكنلوجية

كيف تتعامل مع حرارة الطقس أثناء القيادة؟

لماذا يجب عليك إيقاف تكييف السيارة قبل إطفاء المحرك؟

دراسة تكشف سببا محتملا وراء زيادة خطر إصابة الأطفال بالتوحد

تشيلي.. العثور على متحجرة حيوان ثديي صغير من زمن الديناصورات

المزيد

مواضيع ذات صلة

قصاصات شعر ماكينة الحلاقة الكهربائية وقارب الكافور العائم في الماء

المجاري المائية الرفيعة المتعرجة

أشكال المساحيق

المذبذب الهيدروليكي

الغناء الحَلْقي

صفير أسلاك الهاتف وإبر الصنوبر

التحدث بعد استنشاق الهليوم

صرصرة الرياح

التحدث والغناء

مُذبذب دهن الدجاج

الصافرات والصفير

أصابع زيت الزيتون على الماء المغطى ببودرة التلك