Mathematics contains a number of different systems, but each mathematical system, no matter how different it may be from another, has consistency as one of its goals. When a mathematical system is consistent, a statement and the opposite, or negation, of that same statement cannot both be proven true.

For example, in the familiar system of algebra, it is true that a + 1 >a. Even if a is a negative number, or 0, the statement is true. For example, 3.5 + 1 is 2.5, and 2.5 is greater than 3.5 (because 2.5 is to the right of 3.5 on a number line). Because this system is consistent, it is not possible to prove that a + 1 is less than a or equal to a.

Consistency is also important in the use of mathematical definitions and symbols. For example, (5)²equals 25 and (5)²also equals 25. Is the square root of 25 equal to 5 or to 5? The answer is both: 5 is the square root of 25, and 5 is also the square root of 25.

However, for consistency, the symbol for square root, √ , has been defined to mean only the positive square root, if one exists. So 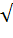25  has only one value (5) even though the equation x²= 25 has two roots, or solutions.

In solving this equation, you must add the± symbol to the radical symbol to show that both the positive and negative roots are desired.

The second step uses the rule that the square root can be taken of both sides of an equation, and the equation will still be true. Is it always true that, if a² =b² , then a = b? Consider the following example.

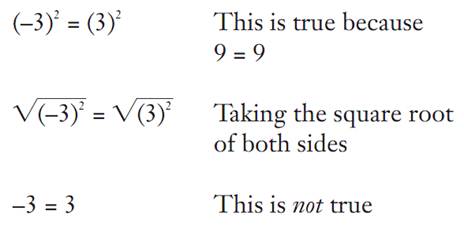
What went wrong? If a²= b², then a = b is consistently true only when a and b are both positive numbers. This means that this rule is true (and the system maintains consistency) if it is written as a²=b² means a= b when a, b ≥ 0.

When moving beyond the familiar systems of ordinary arithmetic and algebra, consistency poses some difficult challenges. For example, many mathematicians have wrestled with the sentence “This statement is not provable.” If the statement is provable, it is false (a contradiction!); if it is true, it is not provable. The work of the mathematicians David Hilbert, Kurt Gödel, Douglas Hofstadter, and Raymond Smullyan delve into this puzzle.

______________________________________________________________________________________________

Reference

Eves, Howard, and Carroll V. Newsom. An Introduction to the Foundations and Fundamental Concepts of Mathematics. New York: Holt, Rinehart, and Winston, 1965.

Hofstadter, Douglas R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books, 1999.

Reid, Constance. Hilbert. Berlin: Springer-Verlag, 1970.

Smullyan, Raymond M. What Is the Name of This Book? The Riddle of Dracula and Other Logical Puzzles. Englewood Cliffs, NJ: Prentice-Hall, 1978.

مواضيع ذات صلة

مجموعة الحل Solution Set

جملة مفتوحة Open Sentence