How equilibria respond to pressure
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص210-211
2025-11-17
42
How equilibria respond to pressure
The equilibrium constant depends on the value of ∆rG0, which is defined at a single, standard pressure. The value of ∆rG0, and hence of K, is therefore independent of the pressure at which the equilibrium is actually established. Formally we may express this independence as
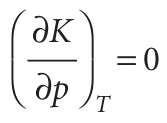
The conclusion that K is independent of pressure does not necessarily mean that the equilibrium composition is independent of the pressure, and its effect depends on how the pressure is applied. The pressure within a reaction vessel can be increased by injecting an inert gas into it. However, so long as the gases are perfect, this addition of gas leaves all the partial pressures of the reacting gases unchanged: the partial pressures of a perfect gas is the pressure it would exert if it were alone in the container, so the presence of another gas has no effect. It follows that pressurization by the addition of an inert gas has no effect on the equilibrium composition of the system (provided the gases are perfect). Alternatively, the pressure of the system may be increased by confining the gases to a smaller volume (that is, by compression). Now the individual partial pressures are changed but their ratio (as it appears in the equilibrium constant) remains the same. Consider, for instance, the perfect gas equilibrium A 5 2 B, for which the equilibrium constant is
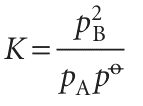
The right-hand side of this expression remains constant only if an increase in pA cancels an increase in the square of pB. This relatively steep increase of pA compared to pB will occur if the equilibrium composition shifts in favour of A at the expense of B. Then the number of A molecules will increase as the volume of the container is decreased and its partial pressure will rise more rapidly than can be ascribed to a simple change in volume alone (Fig. 7.6).
The increase in the number of A molecules and the corresponding decrease in the number of B molecules in the equilibrium A 5 2 B is a special case of a principle proposed by the French chemist Henri Le Chatelier.1 Le Chatelier’s principle states that:
A system at equilibrium, when subjected to a disturbance, responds in a way that tends to minimize the effect of the disturbance The principle implies that, if a system at equilibrium is compressed, then the reaction will adjust so as to minimize the increase in pressure. This it can do by reducing the number of particles in the gas phase, which implies a shift A ← 2 B.
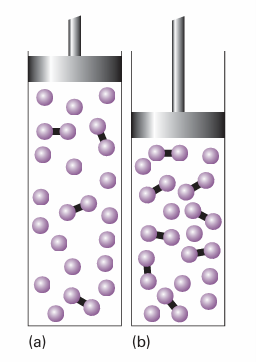
Fig. 7.6 When a reaction at equilibrium is compressed (from a to b), the reaction responds by reducing the number of molecules in the gas phase (in this case by producing the dimers represented by the linked spheres).
To treat the effect of compression quantitatively, we suppose that there is an amount of A present initially (and no B). At equilibrium the amount of A is (1 −α)n and the amount of B is 2αn, where αis the extent of dissociation of A into 2B. It follows that the mole fractions present at equilibrium are
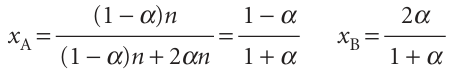
The equilibrium constant for the reaction is
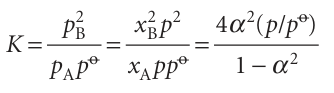
which rearranges to
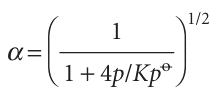
This formula shows that, even though Kis independent of pressure, the amounts of A and B do depend on pressure (Fig. 7.7). It also shows that as p is increased, α decreases, in accord with Le Chatelier’s principle.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
