
Chemical kinetics
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 42
الجزء والصفحة:
Volume I, Chapter 42
 2024-06-05
2024-06-05
 1790
1790
The same situation that we have just called “ionization” is also found in a chemical reaction. For instance, if two objects A and B combine into a compound AB, then if we think about it for a while we see that AB is what we have called an atom, B is what we call an electron, and A is what we call an ion. With these substitutions the equations of equilibrium are exactly the same in form:

This formula, of course, is not exact, since the “constant” c depends on how much volume is allowed for the A and B to combine, and so on, but by thermodynamic arguments one can identify what the meaning of the W in the exponential factor is, and it turns out that it is very close to the energy needed in the reaction.
Suppose that we tried to understand this formula as a result of collisions, much in the way that we understood the evaporation formula, by arguing about how many electrons came off and how many of them came back per unit time. Suppose that A and B combine in a collision every once in a while, to form a compound AB. And suppose that the compound AB is a complicated molecule which jiggles around and is hit by other molecules, and from time to time it gets enough energy to explode and break up again into A and B.

Fig. 42–1.The energy relationship for the reaction A+B→AB.
Now it actually turns out, in chemical reactions, that if the atoms come together with too small an energy, even though energy may be released in the reaction A+B→AB, the fact that A and B may touch each other does not necessarily make the reaction start. It usually is required that the collision be rather hard, in fact, to get the reaction to go at all—a “soft” collision between A and B may not do it, even though energy may be released in the process. So let us suppose that it is very common in chemical reactions that, in order for A and B to form AB, they cannot just hit each other, but they have to hit each other with sufficient energy. This energy is called the activation energy—the energy needed to “activate” the reaction. Call A∗ the activation energy, the excess energy needed in a collision in order that the reaction may really occur. Then the rate Rf at which A and B produce AB would involve the number of atoms of A times the number of atoms of B, times the rate at which a single atom would strike a certain cross section σAB, times a factor e−A∗/kT which is the probability that they have enough energy:
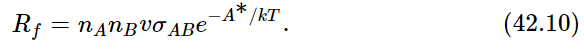
Now we have to find the opposite rate, Rr. There is a certain chance that AB will fly apart. In order to fly apart, it not only must have the energy W which it needs in order to get apart at all but, just as it was hard for A and B to come together, so there is a kind of hill that A and B have to climb over to get apart again; they must have not only enough energy just to get ready to pull apart, but a certain excess. It is like climbing a hill to get into a deep valley; they have to climb the hill coming in and they have to climb out of the valley and then over the hill coming back (Fig. 42–1). Thus, the rate at which AB goes to A and B will be proportional to the number nAB that are present, times e−(W+A∗)/kT:
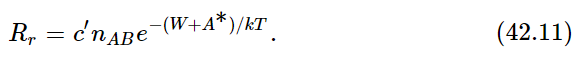
The c′ will involve the volume of atoms and the rate of collisions, which we can work out, as we did the case of evaporation, with areas and times and thicknesses; but we shall not do this. The main feature of interest to us is that when these two rates are equal, the ratio of them is equal to unity. This tells us that nAnB/nAB=ce−W/kT, as before, where c involves the cross sections, velocities, and other factors independent of the n’s.
The interesting thing is that the rate of the reaction also varies as e−const/kT, although the constant is not the same as that which governs the concentrations; the activation energy A∗ is quite different from the energy W. W governs the proportions of A, B, and AB that we have in equilibrium, but if we want to know how fast A+B goes to AB, that is not a question of equilibrium, and here a different energy, the activation energy, governs the rate of reaction through an exponential factor.
Furthermore, A∗ is not a fundamental constant like W. Suppose that at the surface of the wall—or at some other place—A and B could temporarily stick there in such a way that they could combine more easily. In other words, we might find a “tunnel” through the hill, or perhaps a lower hill. By the conservation of energy, when we are all finished, we have still made AB out of A and B, so the energy difference W will be quite independent of the way the reaction occurred, but the activation energy A∗ will depend very much on the way the reaction occurs. This is why the rates of chemical reactions are very sensitive to outside conditions. We can change the rate by putting in a surface of a different kind, we can put it in a “different barrel” and it will go at a different rate, if it depends on the nature of the surface. Or if we put in a third kind of object it may change the rate very much; some things produce enormous changes in rate simply by changing the A∗ a little bit—they are called catalysts. A reaction might practically not occur at all because A∗ is too big at the given temperature, but when we put in this special stuff, the catalyst, then the reaction goes very fast indeed, because A∗ is reduced.
Incidentally, there is some trouble with such a reaction, A plus B, making AB, because we cannot conserve both energy and momentum when we try to put two objects together to make one that is more stable. Therefore, we need at least a third object C, so the actual reaction is much more complicated. The forward rate would involve the product nAnBnC, and it might seem that our formula is going wrong, but no! When we look at the rate at which AB goes the other way, we find that it also needs to collide with C, so there is an nABnC in the reverse rate; the nC’s cancel out in the formula for the equilibrium concentrations. The law of equilibrium, (42.9), which we first wrote down is absolutely guaranteed to be true, no matter what the mechanism of the reaction may be!
 الاكثر قراءة في الفيزياء الكيميائية
الاكثر قراءة في الفيزياء الكيميائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


