Bounded Lattice
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
31-12-2021
1813
Bounded Lattice
A bounded lattice is an algebraic structure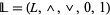 
, such that 
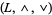is a lattice, and the constants 
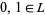satisfy the following:
1. for all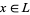 
, 
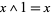and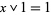 
,
2. for all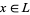 
, 
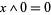and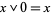 
.
The element 1 is called the upper bound, or top of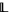 
and the element 0 is called the lower bound or bottom of 
.
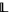There is a natural relationship between bounded lattices and bounded lattice-ordered sets. In particular, given a bounded lattice,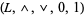 
, the lattice-ordered set 
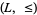that can be defined from the lattice 
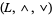is a bounded lattice-ordered set with upper bound 1 and lower bound 0. Also, one may produce from a bounded lattice-ordered set 
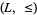a bounded lattice 
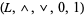in a pedestrian manner, in essentially the same way one obtains a lattice from a lattice-ordered set. Some authors do not distinguish these structures, but here is one fundamental difference between them: A bounded lattice-ordered set 
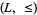can have bounded subposets that are also lattice-ordered, but whose bounds are not the same as the bounds of 
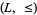; however, any subalgebra of a bounded lattice 
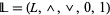is a bounded lattice with the same upper bound and the same lower bound as the bounded lattice 
.
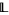For example, let ![X=<span style=]()
{a,b,c}" src="https://mathworld.wolfram.com/images/equations/BoundedLattice/Inline21.gif" style="height:15px; width:74px" />, and let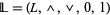 
be the power set of 
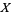, considered as a bounded lattice:
1. ![L=<span style=]()
{emptyset,{a},{b},{c},{a,b},{a,c},{b,c},X}" src="https://mathworld.wolfram.com/images/equations/BoundedLattice/Inline24.gif" style="height:15px; width:256px" />
2. 
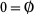and 
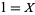
3. 
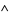is union: for 
, 
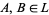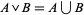
4. 
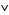is intersection: for 
, 
.
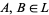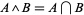Let ![Y=<span style=]()
{a,b}" src="https://mathworld.wolfram.com/images/equations/BoundedLattice/Inline33.gif" style="height:15px; width:58px" />, and let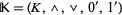 
be the power set of 
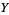, also considered as a bounded lattice:
1. ![K=<span style=]()
{emptyset,{a},{b},Y}" src="https://mathworld.wolfram.com/images/equations/BoundedLattice/Inline36.gif" style="height:15px; width:115px" />
2. 
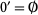and 
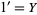
3. 
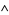is union: for 
, 
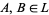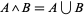
4. 
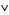is intersection: for 
, 
.
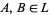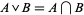Then the lattice-ordered set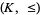 
that is defined by setting 
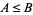iff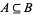 
is a substructure of the lattice-ordered set 
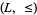that is defined similarly on 
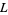. Also, the lattice 
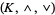is a sublattice of the lattice 
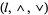. However, the bounded lattice 
is not a subalgebra of the bounded lattice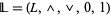 
, precisely because 
.
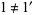الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
