An atlas is a collection of consistent coordinate charts on a manifold, where "consistent" most commonly means that the transition functions of the charts are smooth. As the name suggests, an atlas corresponds to a collection of maps, each of which shows a piece of a manifold and looks like flat Euclidean space. To use an atlas, one needs to know how the maps overlap. To be useful, the maps must not be too different on these overlapping areas.

The overlapping maps from one chart to another are called transition functions. They represent the transition from one chart's point of view to that of another. Let the open unit ball in 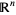 be denoted 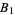. Then if  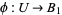and 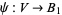 are two coordinate charts, the composition  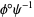is a function defined on 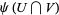. That is, it is a function from an open subset of  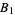to 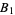, and given such a function from  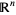to 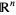, there are conditions for it to be smooth or have  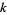smooth derivatives (i.e., it is a C-k function). Furthermore, when  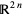is isomorphic to  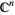(in the even dimensional case), a function can be holomorphic.

A smooth atlas has transition functions that are C-infty smooth (i.e., infinitely differentiable). The consequence is that a smooth function on one chart is smooth in any other chart (by the chain rule for higher derivatives). Similarly, one could have an atlas in class 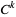, where the transition functions are in class C-k.

In the even-dimensional case, one may ask whether the transition functions are holomorphic. In this case, one has a holomorphic atlas, and by the chain rule, it makes sense to ask if a function on the manifold is holomorphic.

It is possible for two atlases to be compatible, meaning the union is also an atlas. By Zorn's lemma, there always exists a maximal atlas, where a maximal atlas is an atlas not contained in any other atlas. However, in typical applications, it is not necessary to use a maximal atlas and any sufficiently refined atlas will do.