Unknotting Number
المؤلف:
Adams, C. C.
المصدر:
The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman
الجزء والصفحة:
...
15-6-2021
5503
Unknotting Number
The smallest number of times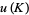 
a knot 
must be passed through itself to untie it. Lower bounds can be computed using relatively straightforward techniques, but it is in general difficult to determine exact values. Many unknotting numbers can be determined from a knot's knot signature. A knot with unknotting number 1 is a prime knot (Scharlemann 1985). It is not always true that the unknotting number is achieved in a projection with the minimal number of crossings.
The following table is from Kirby (1997, pp. 88-89), with the values for 10-139 and 10-152 taken from Kawamura (1998). In the following table, Kirby's (1997, p. 88) value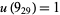 
has been corrected to reflect the fact that 
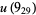is only currently known to be 1 or 2 (Kawauchi 1996, p. 271). The value 
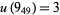has been computed by Stoimenow (2002). The unknotting numbers for 10-154 and 10-161 can be found using the slice-Bennequin inequality (Stoimenow 1998).
Knots for which the unknotting number is not known are 10-11, 10-47, 10-51, 10-54, 10-61, 10-76, 10-77, 10-79, 10-100 (Cha and Livingston 2008).
 |
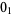0 |
 |
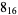2 |
 |
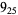2 |
 |
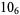3 |
 |
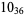2 |
 |
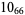3 |
 |
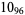2 |
 |
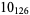2 |
 |
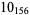1 |
 |
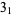1 |
 |
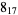1 |
 |
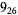1 |
 |
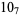1 |
 |
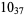2 |
 |
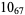2 |
 |
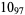2 |
 |
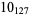2 |
 |
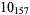2 |
 |
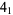1 |
 |
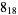2 |
 |
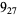1 |
 |
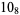2 |
 |
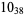2 |
 |
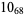2 |
 |
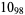2 |
 |
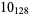3 |
 |
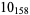2 |
 |
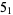2 |
 |
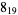3 |
 |
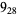1 |
 |
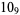1 |
 |
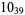2 |
 |
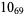2 |
 |
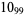2 |
 |
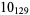1 |
 |
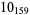1 |
 |
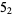1 |
 |
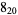1 |
 |
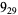2 |
 |
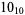1 |
 |
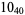2 |
 |
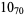2 |
 |
? |
 |
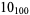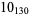2 |
 |
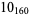2 |
 |
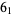1 |
 |
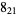1 |
 |
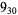1 |
 |
? |
 |
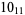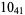2 |
 |
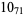1 |
 |
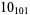3 |
 |
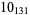1 |
 |
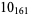3 |
 |
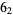1 |
 |
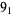4 |
 |
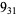2 |
 |
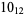2 |
 |
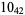1 |
 |
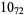2 |
 |
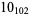1 |
 |
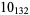1 |
 |
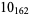2 |
 |
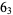1 |
 |
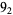1 |
 |
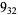2 |
 |
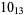2 |
 |
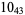2 |
 |
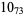1 |
 |
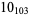3 |
 |
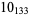1 |
 |
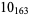2 |
 |
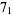3 |
 |
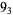3 |
 |
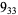1 |
 |
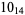2 |
 |
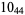1 |
 |
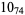2 |
 |
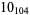1 |
 |
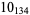3 |
 |
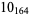1 |
 |
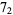1 |
 |
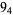2 |
 |
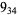1 |
 |
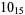2 |
 |
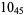2 |
 |
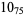2 |
 |
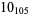2 |
 |
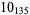2 |
 |
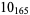2 |
 |
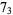2 |
 |
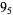2 |
 |
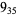3 |
 |
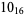2 |
 |
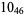3 |
 |
? |
 |
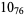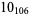2 |
 |
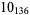1 |
|
|
 |
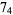2 |
 |
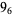3 |
 |
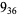2 |
 |
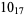1 |
 |
? |
 |
? |
 |
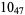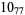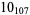1 |
 |
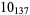1 |
|
|
 |
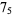2 |
 |
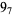2 |
 |
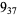2 |
 |
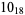1 |
 |
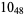2 |
 |
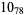2 |
 |
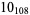2 |
 |
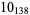2 |
|
|
 |
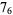1 |
 |
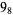2 |
 |
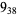3 |
 |
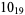2 |
 |
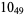3 |
 |
? |
 |
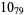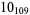2 |
 |
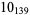4 |
|
|
 |
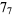1 |
 |
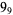3 |
 |
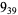1 |
 |
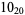2 |
 |
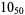2 |
 |
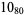3 |
 |
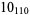2 |
 |
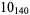2 |
|
|
 |
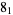1 |
 |
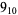3 |
 |
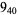2 |
 |
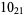2 |
 |
? |
 |
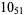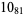2 |
 |
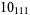2 |
 |
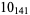1 |
|
|
 |
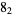2 |
 |
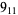2 |
 |
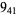2 |
 |
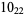2 |
 |
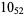2 |
 |
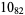1 |
 |
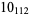2 |
 |
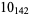3 |
|
|
 |
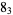2 |
 |
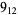1 |
 |
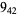1 |
 |
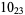1 |
 |
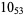3 |
 |
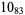2 |
 |
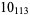1 |
 |
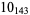1 |
|
|
 |
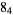2 |
 |
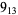3 |
 |
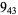2 |
 |
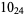2 |
 |
? |
 |
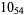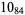1 |
 |
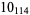1 |
 |
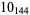2 |
|
|
 |
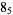2 |
 |
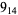1 |
 |
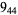1 |
 |
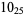2 |
 |
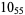2 |
 |
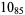2 |
 |
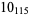2 |
 |
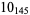2 |
|
|
 |
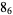2 |
 |
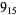2 |
 |
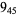1 |
 |
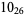1 |
 |
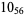2 |
 |
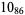2 |
 |
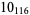2 |
 |
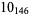1 |
|
|
 |
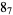1 |
 |
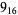3 |
 |
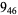2 |
 |
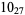1 |
 |
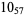2 |
 |
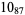2 |
 |
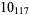2 |
 |
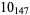1 |
|
|
 |
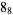2 |
 |
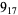2 |
 |
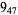2 |
 |
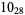2 |
 |
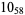2 |
 |
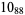1 |
 |
1 |
 |
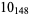2 |
|
|
 |
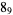1 |
 |
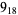2 |
 |
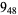2 |
 |
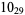2 |
 |
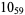1 |
 |
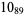2 |
 |
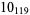1 |
 |
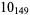2 |
|
|
 |
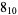2 |
 |
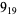1 |
 |
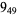3 |
 |
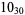1 |
 |
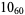1 |
 |
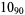2 |
 |
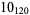3 |
 |
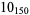2 |
|
|
 |
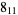1 |
 |
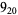2 |
 |
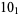1 |
 |
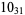1 |
 |
? |
 |
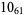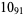1 |
 |
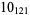2 |
 |
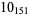2 |
|
|
 |
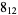2 |
 |
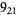1 |
 |
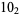3 |
 |
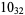1 |
 |
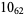2 |
 |
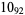2 |
 |
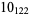2 |
 |
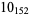4 |
|
|
 |
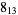1 |
 |
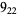1 |
 |
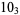2 |
 |
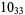1 |
 |
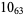2 |
 |
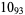2 |
 |
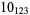2 |
 |
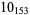2 |
|
|
 |
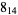1 |
 |
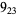2 |
 |
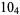2 |
 |
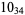2 |
 |
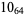2 |
 |
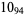2 |
 |
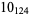4 |
 |
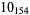3 |
|
|
 |
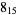2 |
 |
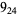1 |
 |
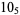2 |
 |
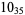2 |
 |
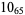2 |
 |
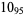1 |
 |
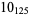2 |
 |
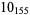2 |
|
|
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 57-64, 1994.
Cha, J. C. and Livingston, C. "Unknown Values in the Table of Knots." 2008 May 16. https://arxiv.org/abs/math.GT/0503125.
Cipra, B. "From Knot to Unknot." What's Happening in the Mathematical Sciences, Vol. 2. Providence, RI: Amer. Math. Soc., pp. 8-13, 1994.
Kawamura, T. "The Unknotting Numbers of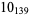 
and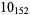 
Are 4." Osaka J. Math. 35, 539-546, 1998.
Kawauchi, A. "Knot Invariants." Appendix F.3 in A Survey of Knot Theory. Boston: Birkhäuser, 1996.
Kirby, R. (Ed.). "Problems in Low-Dimensional Topology." AMS/IP Stud. Adv. Math., 2.2, Geometric Topology (Athens, GA, 1993). Providence, RI: Amer. Math. Soc., pp. 35-473, 1997.
Scharlemann, M. "Unknotting Number One Knots Are Prime." Invent. Math. 82, 37-55, 1985.
Stoimenow, A. "Polynomial Values, the Linking Form, and Unknotting Numbers." https://www.math.toronto.edu/stoimeno/goer.ps.gz. Feb. 10, 2002.
Stoimenow, A. "Positive Knots, Closed Braids and the Jones Polynomial." https://www.math.toronto.edu/stoimeno/pos.ps.gz. Mar. 2, 2002.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
