A connection on a vector bundle 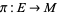 is a way to "differentiate" bundle sections, in a way that is analogous to the exterior derivative  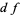of a function 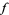. In particular, a connection  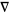is a function from smooth sections  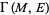to smooth sections of  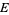with one-forms  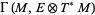that satisfies the following conditions.

1. 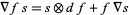 (Leibniz rule), and

2. .

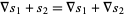Alternatively, a connection can be considered as a linear map from bundle sections of 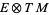, i.e., a section of  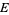with a vector field 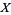, to sections of 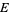, in analogy to the directional derivative. The directional derivative of a function 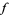, in the direction of a vector field 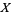, is given by 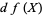. The connection, along with a vector field 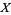, may be applied to a section  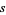of 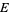 to get the section 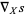. From this perspective, connections must also satisfy

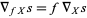(1)

for any smooth function 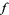. This property follows from the first definition.

For example, the trivial bundle 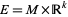 admits a flat connection since any bundle section  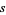corresponds to a function 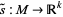. Then setting  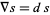gives the connection. Any connection on the trivial bundle is of the form 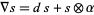, where  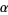is any one-form with values in 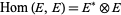, i.e.,  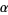is a matrix of one-forms.

The matrix of one-forms

(2)

determines a connection 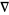 on the rank-3 bundle over 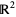. It acts on a section  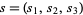by the following.

			(3)
			(4)
			(5)
			(6)
			(7)
			(8)

In any trivialization, a connection can be described just as in the case of a trivial bundle. However, if the bundle 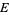 is not trivial, then the exterior derivative  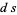is not well-defined (globally) for a bundle section 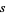. Still, the difference between any two connections must be one-forms with values in endomorphisms of 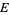,i.e., matrices of one forms. So the space of connections forms an affine space.

The bundle curvature of the bundle is given by the formula 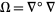. In coordinates,  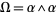is matrix of two-forms. For instance, in the example above,

(9)

is the curvature.

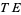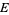Another way of describing a connection is as a splitting of the tangent bundle  of  as 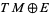. The vertical part of  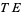corresponds to tangent vectors along the fibers, and is the kernel of 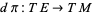. The horizontal part is not well-defined a priori. A connection defines a subspace of  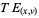which is isomorphic to 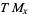. It defines  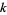flat sections  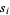such that 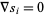, which are a vector basis for the fiber bundles of 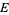, at least nearby . These flat sections determine the horizontal part of 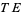 near . Also, a connection on a vector bundle can be defined by a principal bundle connection on the associated principal bundle.

In some settings there is a canonical connection. For example, a Riemannian manifold has the Levi-Civita connection, given by the Christoffel symbols of the first and second kinds, which is the unique torsion-free connection compatible with the metric. A holomorphic vector bundle with a Hermitian metric has a unique connection which is compatible with both metric and the complex structure.