Definition A chain complex C_∗ is a (doubly infinite) sequence (C_i: i ∈ Z) of modules over some unital ring, together with homomorphisms ∂_I : C_i → C_i−1 for each i ∈ Z, such that ∂_i ◦ ∂_i+1 = 0 for all integers i.

The ith homology group H_i(C_∗) of the complex C_∗ is defined to be the quotient group Z_i(C_∗)/B_i(C_∗), where Z_i(C_∗) is the kernel of ∂_i: C_i → C_i−1 and B_i(C_∗) is the image of ∂_i+1: C_i+1 → C_i .

Note that if the modules C_∗ occuring in a chain complex C_∗ are modules over some unital ring R then the homology groups of the complex are also modules over this ring R.

Definition Let C_∗ and D_∗ be chain complexes. A chain map f: C_∗ → D_∗ isa sequence f_i: C_i → D_i of homomorphisms which satisfy the commutativity condition ∂_i ◦ f_i = f_i−1 ◦ ∂_ifor all i ∈ Z.

Note that a collection of homomorphisms f_i : C_i → D_i defines a chain map f_∗: C_∗ → D_∗ if and only if the diagram

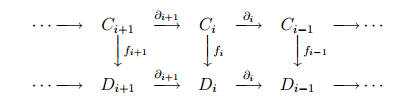
is commutative.

Let C_∗ and D_∗ be chain complexes, and let f_∗: C_∗ → D_∗ be a chain map.

Then f_i(Z_i(C_∗)) ⊂ Z_i(D_∗) and f_i(B_i(C_∗)) ⊂ B_i(D_∗) for all i. It follows from this that f_i : C_i → D_i induces a homomorphism f_∗: H_i(C_∗) → H_i(D_∗) of homology groups sending [z] to [f_i(z)] for all z ∈ Z_i(C_∗), where [z] = z + B_i(C_∗), and [f_i(z)] = f_i(z) + B_i(D_∗).

Definition A short exact sequence 0−→A_∗  ^p∗→B_∗ ^q∗→C_∗→0 of chain complexes consists of chain complexes A_∗, B_∗ and C_∗ and chain maps p_∗: A_∗ → B_∗ and q_∗: B_∗ → C_∗ such that the sequence

0→A_i    ^pi →B_i  ^qi→C_i→0

is exact for each integer i.

We see that 0→A_∗^p∗ −→B_∗^q∗→C_∗→0 is a short exact sequence of chain complexes if and only if the diagram

Lemma 1.1 Given any short exact sequence 0→A_∗^p∗→B_∗^q∗→C_∗→0 of chain complexes, there is a well-defined homomorphism

                               α_i: H_i(C_∗) → H_i−1(A_∗)

which sends the homology class [z] of z ∈ Z_i(C_∗) to the homology class [w] of any element w of Z_i−1(A_∗) with the property that p_i−1(w) = ∂_i(b) for some b ∈ B_i satisfying q_i(b) = z.

Proof Let z ∈ Z_i(C_∗). Then there exists b ∈ Bi satisfying q_i(b) = z, since

q_i: B_i → C_i   is surjective. Moreover

                         q_i−1(∂_i(b)) = ∂_i(q_i(b)) = ∂_i(z) = 0.

But p_i−1: A_i−1 → B_i−1 is injective and p_i−1(A_i−1) = ker q_i−1, since the sequence

                                 0−→A_i−1   ^pi−1−→B_i−1 ^qi−1→C_i−1

is exact. Therefore there exists a unique element w of A_i−1 such that ∂_i(b) =p_i−1(w). Moreover

                     p_i−2(∂_i−1(w)) = ∂_i−1(p_i−1(w)) = ∂_i−1(∂_i(b)) = 0

(since ∂_i−1 ◦ ∂_i = 0), and therefore ∂_i−1(w) = 0 (since p_i−2: A_i−2 → B_i−2 is injective). Thus w ∈ Z_i−1(A_∗).

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

Triple Torus

Thurston Elliptization Conjecture

Thurston,s Geometrization Conjecture

Real Projective Plane

Pseudometric Topology

Pseudocrosscap

Parallelizable

Möbius Strip

Möbius Shorts

Path

Product Topology

Handle