
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Membrane interpretation
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 168
2-2-2017
1881
Membrane interpretation
1.1 Maxwell’s equations in (3 + 1)-form
we define a set of observers in the Kerr spacetime which have the four-velocity uμ such that
 (1.1)
(1.1)
where α := (ΣΔ/A)1/2 is the lapse function. Since uμξμ(φ)= 0, this family of observers has zero angular momentum. By means of the projector hμν = gμν + uμuν we can obtain spatial vectors and tensors in the reference frame of the observer.
We introduce the following notation for the so defined electrodynamical quantities measured by locally non-rotating observers: E is the electric field strength, B is the magnetic field strength, ρe is the electric charge density, and j is the electric current density. Denote by ϖ the norm of a Killing vector ξμ(φ) reflecting the axial symmetry of spacetime,
 (1.2)
(1.2)
We denote by eǿ a three dimensional unit vector in the direction of the Killing vector ξμ(φ). By using this notation, Maxwell's equations can be written in the following form:
 (1.3)
(1.3)
∇B = 0 (1.4)
 (1.5)
(1.5)
 (1.6)
(1.6)
Here
 (1.7)
(1.7)
and
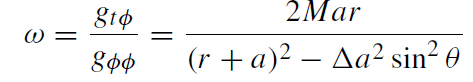 (1.8)
(1.8)
is the angular velocity of rotation (with respect to t) of locally non-rotating observers. The notation ʆβE is used for the Lie derivative of a vector E along β
 (1.9)
(1.9)
This Lie derivative describes how the vector E varies with respect to the field β. ʆβE vanishes when the origin and the end of the vector E are ‘glued’ under a displacement by β dφ. A dot denotes differentiation with respect to t and ∇ is the three dimensional (covariant) gradient operator in the curved ‘absolute’ space with metric hμν .
The equations (1.3), (1.4) have a familiar form, whereas (1.5), (1.6) are slightly unusual. The following differences are evident. The function α appears because the physical time flows differently at different points of space while the equations are written in terms of the global ‘time’ t (recall that the acceleration of free fall, a, is related to α in the reference frame of locally nonrotating observers by the formula a = −c2∇ ln α). Furthermore, the expressions in brackets are ‘Lie-type’ derivatives (with respect to time) for the set of locally non-rotating observers who move in absolute space and for whom dx/dt = β.
Thus, these expressions correspond to total derivatives with respect to the times of E and B, respectively, with the motion of locally non-rotating observers taken into account.
1.2 Boundary conditions at the event horizon
The Rindler spacetime is a very good approximation in the narrow strip region near the event horizon of a black hole. For this reason, the previous results can be easily generalized to the case of a stationary black hole.
The event horizon is generated by null geodesics which are bicharacteristics of Maxwell's equations. The corresponding boundary conditions at the horizon can be written in a very clear form by introducing a fictitious surface electric charge density σ H which compensates for the flux of the electric field across the surface and a fictitious surface electric current iH which closes tangent components of the magnetic fields at the horizon. This interpretation is used in the membrane formalism.
The horizon of a stationary black hole has topology T × S2, and the surface with the topology S2 is a two dimensional surface of infinite gravitational redshift, α = 0. The redshifted gravitational acceleration αa ≡ −c2αn ln α remains finite at the horizon:
 (1.10)
(1.10)
where n is a unit vector pointing orthogonally out of the horizon, and κ is the surface gravity. In the context of calculations near the horizon, it is convenient to introduce a coordinate system (α, λ, φ), where λ is a proper distance along the horizon from the north pole toward the equator. In these coordinates, the metric of the absolute three-space near the horizon takes the form
 (1.11)
(1.11)
and the unit vectors along the ‘toroidal’ (φ), ‘poloidal’ (λ), and ‘normal’ (α) directions are
 (1.12)
(1.12)
Macdonald and Thorne formulated the conditions at the horizon as follows:
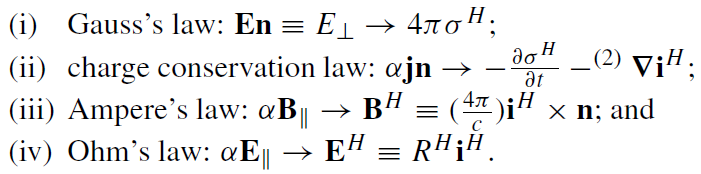
In these relations the symbol→ indicates approach to the black hole horizon along the trajectory of a freely falling observer; (2)∇ is the two-dimensional divergence at the horizon, and B|| and E|| are the magnetic and electric field components tangent to the horizon. RH ≡ 4π/c is the effective surface resistance of the event horizon (RH = 377Ω). The lapse function α in the conditions reflects the slowdown in the flow of physical time for locally non-rotating observers in the neighborhood of the black hole.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















