
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Black hole in a magnetic field
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 172
2-2-2017
1950
Black hole in a magnetic field
1.1 Killing vectors and Maxwell fields
Let us discuss now properties of a black hole immersed in an external magnetic field which is homogenous at infinity. We consider the magnetic field as a test field and neglect its back reaction. This problem allows an elegant solution based on the properties of Killing vector fields. We proceed as follows: a Killing vector in a vacuum spacetime generates a solution of Maxwell's equations. Let us put
 (1.1)
(1.1)
then
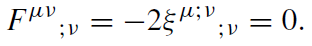 (1.2)
(1.2)
The commutator of two covariant derivatives turns out to be (Ricci identity)
 (1.3)
(1.3)
Permuting over the indices μ, ν, and σ, adding the resulting terms, using the Killing equation and the symmetries of the Riemann tensor, one gets
 (1.4)
(1.4)
By contracting the indices ν and σ, we obtain
 (1.5)
(1.5)
In a vacuum spacetime we have Rμλ = 0 and hence Fμν associated with the Killing vector ξμ satisfies the homogeneous Maxwell equation.
1.2 A black hole in a homogeneous magnetic field
The relation between the Killing vector and an electromagnetic field in Kerr geometry can be used to construct a solution describing a magnetic test field, which is homogeneous at infinity. Let us introduce two fields:
 (1.6)
(1.6)
At large distances F(t)μν vanishes, while F(φ)μν asymptotically becomes a uniform magnetic field.
It is easy to show that for any two-dimensional surface Σ surrounding a black hole
 (1.7)
(1.7)
for both fields. Thus the magnetic monopole charge vanishes for both solutions. One also has
 (1.8)
(1.8)
Here ∗F(t)μν = Ɛμναβ Fαβ. Thus, the axial Killing vector ξ(φ) generates a stationary, axisymmetric field, which asymptotically approaches a uniform magnetic field and, moreover, has electric charge 4aM. The timelike Killing vector ξ(t ) generates a stationary, axisymmetric field, which vanishes at infinity and has electric charge −2M.
Combining these results we conclude that for a neutral black hole the electromagnetic field which asymptotically approaches the homogeneous magnetic field B is given by the vector potential
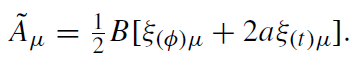 (1.9)
(1.9)
The electrostatic injection energy per unit charge calculated along the symmetry axis is
 (1.10)
(1.10)
Carter proved that ϵ is constant over the event horizon. Thus a black hole immersed in a rarefied plasma will accrete charge until ϵ vanishes. The resulting black hole charge is
Q = 2BaM. (1.11)
The vector potential for such a black hole is
 (5.12)
(5.12)
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















