
BLACKBODY RADIATION AND THE STEFAN–BOLTZMANN LAW
 المؤلف:
Mark Csele
المؤلف:
Mark Csele
 المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
 الجزء والصفحة:
p2
الجزء والصفحة:
p2
 7-3-2016
7-3-2016
 2884
2884
BLACKBODY RADIATION AND THE STEFAN–BOLTZMANN LAW
Imagine a substance that absorbs all incident light, of all frequencies, shining on it. Such an object would reflect no light whatsoever and would appear to be completely black—hence the term blackbody. If the blackbody is now heated to the point where it glows (called incandescence), emissions from the object should, in theory, be as perfect as its absorption—one would logically expect it to emit light at all frequencies since it absorbs at all frequencies. In the 1850s a physicist named Kirchhoff, a pioneer in the use of spectroscopy as a tool for chemical analysis, observed that real substances absorb better at some frequencies than others. When heated, those substances emitted more light at those frequencies. The paradox spawned research into radiation in general and specifically, how radiation emitted from an object varied with temperature. It was observed that the amount of radiation emitted from an object varied with the temperature of the object. The mathematical relationship for this dependence on temperature was established in 1879 by the physicist Josef Stefan, who showed that the total energy radiated by an object increased as the fourth power of the temperature of the object. All objects at a temperature above absolute zero (0 K) radiate energy, and when the temperature of an object is doubled, the total amount of energy radiated from the object will be 16 times as great! In 1884, Ludwig Boltzmann completed the mathematical picture of a blackbody radiator, and the Stefan–Boltzmann law was developed, which allows calculation of the total energy integrated over a blackbody spectrum.
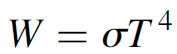 (1.1)
(1.1)
where s is the Stefan–Boltzmann constant (=5.67 × 10-8 W/m2 .K4) and T is the temperature in kelvin. This law applies, strictly speaking, to ideal blackbodies. For a non-ideal blackbody radiator, a third term, called the emissivity of an object, is added, so the law becomes
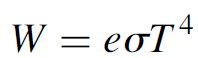 (1.2)
(1.2)
where the emissivity of the object (e) is a measure of how well it radiates energy. An ideal blackbody has a value of 1; real objects have a value between 0 and 1.
Example 1.1 Use of the Stefan–Boltzmann Formula The Stefan–Boltzmann formula gives an answer in watts per square meter. This can be rearranged to give the power output of an object as
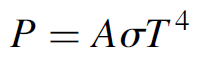
where A is the surface area of the object. Now consider two objects: The first is a large (1-m2) object at a relatively cool temperature of 300 K. The total power radiated from this (ideal) object is 459 W. Now consider a much smaller (10 cm2 = 1 × 10-4 m2) object at 3000 K. The total power radiated from this object is also 459 W. Although 10,000 times smaller, the object is also much hotter, so radiates a great deal of power. Perhaps the most startling revelation from all this is that the 1-m2 object at room temperature emits 459 W at all. This may seem like an enormous amount of energy, especially when compared to a 500-W floodlight; however, essentially all of this output is in the far-infrared region of the spectrum and is manifested as heat. The human body, similarly, emits a fair quantity of heat (hence the reason for large air conditioners in office buildings that house large quantities of bodies in a relatively confined space).
 الاكثر قراءة في الضوء
الاكثر قراءة في الضوء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


