تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Fractals
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
144-149
22-2-2016
1842
In March 1980, the state-of-the-art mainframe computer at the IBM research centre at Yorktown Heights, New York State, was issuing its instructions to an ancient Tektronix printing device. It dutifully struck dots in curious places on a white page, and when it had stopped its clatter the result looked like a handful of dust smudged across the sheet. Benoît Mandelbrot rubbed his eyes in disbelief. He saw it was important, but what was it? The image that slowly appeared before him was like the black and white print emerging from a photographic developing bath. It was a first glimpse of that icon in the world of fractals – the Mandelbrot set.
This was experimental mathematics par excellence, an approach to the subject in which mathematicians had their laboratory benches just like the physicists and chemists. They too could now do experiments. New vistas opened up – literally. It was a liberation from the arid climes of ‘definition, theorem, proof’, though a return to the rigours of rational argument would have to come albeit later.
The downside of this experimental approach was that the visual images preceded a theoretical underpinning. Experimentalists were navigating without a map. Although Mandelbrot coined the word ‘fractals’, what were they? Could there be a precise definition for them in the usual way of mathematics? In the beginning, Mandelbrot didn’t want to do this. He didn’t want to destroy the magic of the experience by honing a sharp definition which might be inadequate and limiting. He felt the notion of a fractal, ‘like a good wine – demanded a bit of aging before being “bottled”.’
The Mandelbrot set
Mandelbrot and his colleagues were not being particularly abstruse mathematicians. They were playing with the simplest of formulae. The whole idea is based on iteration – the practice of applying a formula time and time again. The formula which generated the Mandelbrot set was simply x2 + c.
The first thing we do is choose a value of c. Let’s choose c = 0.5. Starting with x = 0 we substitute into the formula x2 + 0.5. This first calculation gives 0.5 again. We now use this as x, substituting it into x2 + 0.5 to give a second calculation: (0.5)2 + 0.5 = 0.75. We keep going, and at the third stage this will be (0.75)2 + 0.5 = 1.0625. All these calculations can be done on a handheld calculator. Carrying on we find that the answer gets bigger and bigger.
Let’s try another value of c, this time c = – 0.5. As before we start at x = 0 and substitute it into x2 – 0.5 to give – 0.5. Carrying on we get – 0.25, but this time the values do not become bigger and bigger but, after some oscillations, settle down to a figure near – 0.3660. . .
So by choosing c = 0.5 the sequence starting at x = 0 zooms off to infinity, but by choosing c = – 0.5 we find that the sequence starting at x = 0 actually converges to a value near – 0.3660. The Mandelbrot set consists of all those values of c for which the sequence starting at x = 0 does not escape to infinity.
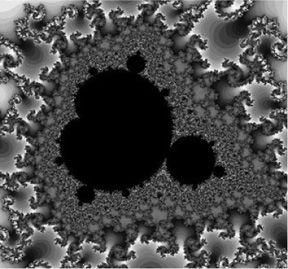
The Mandelbrot set
This is not the whole story because so far we have only considered the one-dimensional real numbers – giving a one-dimensional Mandelbrot set so we wouldn’t see much. What needs to be considered is the same formula z2 + c but with z and c as two-dimensional complex numbers . This will give us a two-dimensional Mandelbrot set.
For some values of c in the Mandelbrot set, the sequence of zs may do all sorts of strange things like dance between a number of points but they will not escape to infinity. In the Mandelbrot set we see another key property of fractals, that of self-similarity. If you zoom into the set you will not be sure of the level of magnification because you will just see more Mandelbrot sets.
Before Mandelbrot
Like most things in mathematics, discoveries are rarely brand new. Looking into the history Mandelbrot found that mathematicians such as Henri Poincaré and Arthur Cayley had brief glimmerings of the idea a hundred years before him. Unfortunately they did not have the computing power to investigate matters further.
The shapes discovered by the first wave of fractal theorists included crinkly curves and the ‘monster curves’ that had previously been dismissed as pathological examples of curves. As they were so pathological they had been locked up in the mathematician’s cupboard and given little attention. What was wanted then were the more normal ‘smooth’ curves which could be dealt with by the differential calculus. With the popularity of fractals, other mathematicians whose work was resurrected were Gaston Julia and Pierre Fatou who worked on fractal-like structures in the complex plane in the years following the First World War. Their curves were not called fractals, of course, and they did not have the technological equipment to see their shapes.
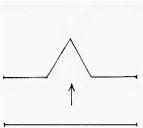
The generating element of the Koch snowflake
Other famous fractals
The famous Koch curve is named after the Swedish mathematician Niels Fabian Helge von Koch. The snowflake curve is practically the first fractal curve. It is generated from the side of the triangle treated as an element, splitting it into three parts each of length ⅓ and adding a triangle in the middle position.

The Koch snowflake
The curious property of the Koch curve is that it has a finite area, because it always stays within a circle, but at each stage of its generation its length increases. It is a curve which encloses a finite area but has an ‘infinite’ circumference!
Another famous fractal is named after the Polish mathematician Wacław Sierpinski. It is found by subtracting triangles from an equilateral triangle; and by continuing this process, we get the Sierpinski gasket.
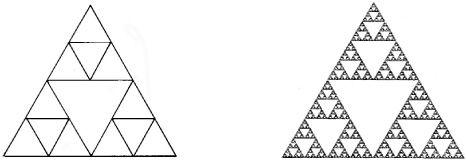
The Sierpin ski gasket
Fractional dimension
The way Felix Hausdorff looked at dimension was innovative. It has to do with scale. If a line is scaled up by a factor of 3 it is 3 times longer than it was previously. Since this 3 = 31 a line is said to have dimension 1. If a solid square is scaled up by a factor of 3 its area is 9 times its previous value or 32 and so the dimension is 2. If a cube is scaled up by this factor its volume is 27 or 33 times its previous value, so its dimension is 3. These values of the Hausdorff dimension all coincide with our expectations for a line, square, or cube.
If the basic unit of the Koch curve is scaled up by 3, it becomes 4 times longer than it was before. Following the scheme described, the Hausdorff dimension is the value of D for which 4 = 3D. An alternative calculation is that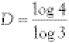
which means that D for the Koch curve is approximately 1.262. With fractals it is frequently the case that the Hausdorff dimension is greater than the ordinary dimension, which is 1 in the case of Koch curve.
The Hausdorff dimension informed Mandelbrot’s definition of a fractal – a set of points whose value of D is not a whole number. Fractional dimension became the key property of fractals.
The applications of fractals
The potential for the applications of fractals is wide. Fractals could well be the mathematical medium which models such natural objects as plant growth, or cloud formation.
Fractals have already been applied to the growth of marine organisms such as corals and sponges. The spread of modern cities has been shown to have a similarity with fractal growth. In medicine they have found application in the modelling of brain activity. And the fractal nature of movements of stocks and shares and the foreign exchange markets has also been investigated. Mandelbrot’s work opened up a new vista and there is much still to be discovered.
the condensed idea
Shapes with fractional dimension

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)