We now turn to an interesting analogous situation having to do with the blackbody radiation law. In the last chapter we worked out the distribution law for the radiation in a cavity the way Planck did, considering the radiation from an oscillator. The oscillator had to have a certain mean energy, and since it was oscillating, it would radiate and would keep pumping radiation into the cavity until it piled up enough radiation to balance the absorption and emission. In that way we found that the intensity of radiation at frequency ω was given by the formula

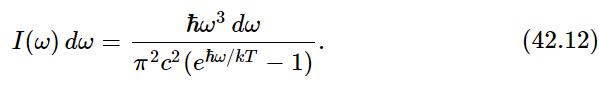
This result involved the assumption that the oscillator which was generating the radiation had definite, equally spaced energy levels. We did not say that light had to be a photon or anything like that. There was no discussion about how, when an atom goes from one level to another, the energy must come out in one unit of energy, ℏω, in the form of light. Planck’s original idea was that the matter was quantized but not the light: material oscillators cannot take up just any energy, but have to take it in lumps. Furthermore, the trouble with the derivation is that it was partially classical. We calculated the rate of radiation from an oscillator according to classical physics; then we turned around and said, “No, this oscillator has a lot of energy levels.” So gradually, in order to find the right result, the completely quantum-mechanical result, there was a slow development which culminated in the quantum mechanics of 1927. But in the meantime, there was an attempt by Einstein to convert Planck’s viewpoint that only oscillators of matter were quantized, to the idea that light was really photons and could be considered in a certain way as particles with energy ℏω. Furthermore, Bohr had pointed out that any system of atoms has energy levels, but they are not necessarily equally spaced like Planck’s oscillator. And so, it became necessary to rederive or at least rediscuss the radiation law from a more completely quantum-mechanical viewpoint.

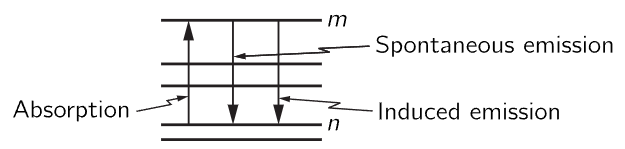
Fig. 42–2. Transitions between two energy levels of an atom.

Einstein assumed that Planck’s final formula was right, and he used that formula to obtain some new information, previously unknown, about the interaction of radiation with matter. His discussion went as follows: Consider any two of the many energy levels of an atom, say the mth level and the nth level (Fig. 42–2). Now Einstein proposed that when such an atom has light of the right frequency shining on it, it can absorb that photon of light and make a transition from state n to state m, and that the probability that this occurs per second depends upon the two levels, of course, but is proportional to how intense the light is that is shining on it. Let us call the proportionality constant B_nm, merely to remind us that this is not a universal constant of nature, but depends on the particular pair of levels: some levels are easy to excite; some levels are hard to excite. Now what is the formula going to be for the rate of emission from m to n? Einstein proposed that this must have two parts to it. First, even if there were no light present, there would be some chance that an atom in an excited state would fall to a lower state, emitting a photon; this we call spontaneous emission. It is analogous to the idea that an oscillator with a certain amount of energy, even in classical physics, does not keep that energy, but loses it by radiation. Thus, the analog of spontaneous radiation of a classical system is that if the atom is in an excited state there is a certain probability A_mn, which depends on the levels again, for it to go down from m to n, and this probability is independent of whether light is shining on the atom or not. But then Einstein went further, and by comparison with the classical theory and by other arguments, concluded that emission was also influenced by the presence of light—that when light of the right frequency is shining on an atom, it has an increased rate of emitting a photon that is proportional to the intensity of the light, with a proportionality constant B_mn. Later, if we deduce that this coefficient is zero, then we will have found that Einstein was wrong. Of course we will find he was right.

Thus, Einstein assumed that there are three kinds of processes: an absorption proportional to the intensity of light, an emission proportional to the intensity of light, called induced emission or sometimes stimulated emission, and a spontaneous emission independent of light.

Now suppose that we have, in equilibrium at temperature T, a certain number of atoms N_n in the state n and another number N_m in the state m. Then the total number of atoms that are going from n to m is the number that are in the state n times the rate per second that, if one is in n, it goes up to m. So we have a formula for the number that are going from n to m per second:

The number that will go from m to n is expressed in the same manner, as the number N_m that are in m, times the chance per second that each one goes down to n. This time our expression is

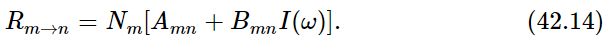
Now we shall suppose that in thermal equilibrium the number of atoms going up must equal the number coming down. That is one way, at least, in which the number will be sure to stay constant in each level. ¹ So we take these two rates to be equal at equilibrium. But we have one other piece of information: we know how large N_m is compared with N_n—the ratio of those two is e^−(E_m^−E_n^)/kT. Now Einstein assumed that the only light which is effective in making the transition from n to m is the light which has the frequency corresponding to the energy difference, so E_m−E_n=ℏω in all our formulas. Thus

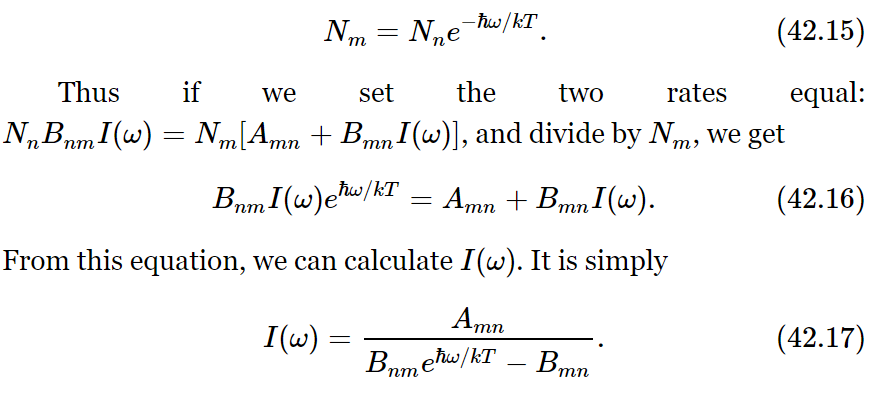
But Planck has already told us that the formula must be (42.12). Therefore, we can deduce something: First, that B_nm must equal B_mn, since otherwise we cannot get the (e^ℏω/kT−1). So, Einstein discovered some things that he did not know how to calculate, namely that the induced emission probability and the absorption probability must be equal. This is interesting. And furthermore, in order for (42.17) and (42.12) to agree,

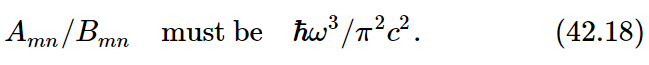
So if we know, for instance, the absorption rate for a given level, we can deduce the spontaneous emission rate and the induced emission rate, or any combination.

This is as far as Einstein or anyone else could go using such arguments. To actually compute the absolute spontaneous emission rate or the other rates for any specific atomic transition, of course, requires a knowledge of the machinery of the atom, called quantum electrodynamics, which was not discovered until eleven years later. This work of Einstein was done in 1916.

The possibility of induced emission has, today, found interesting applications. If there is light present, it will tend to induce the downward transition. The transition then adds its ℏω to the available light energy, if there were some atoms sitting in the upper state. Now we can arrange, by some nonthermal method, to have a gas in which the number in the state m is very much greater than the number in the state n. This is far out of equilibrium, and so is not given by the formula e^−ℏω/kT, which is for equilibrium. We can even arrange it so that the number in the upper state is very large, while the number in the lower state is practically zero. Then light which has the frequency corresponding to the energy difference E_m−E_n will not be strongly absorbed, because there are not many atoms in state n to absorb it. On the other hand, when that light is present, it will induce the emission from this upper state! So, if we had a lot of atoms in the upper state, there would be a sort of chain reaction, in which, the moment the atoms began to emit, more would be caused to emit, and the whole lot of them would dump down together. This is what is called a laser, or, in the case of the far infrared, a maser.

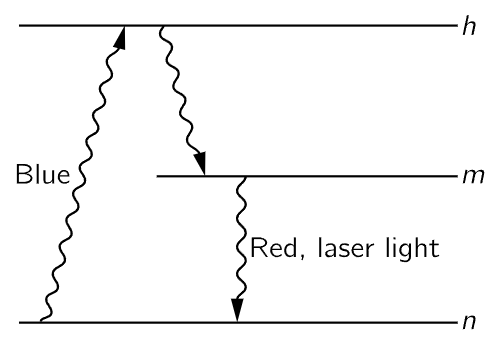
Fig. 42–3. By exciting, say by blue light, a higher state h, which may emit a photon leaving atoms in state m, the number in this state m becomes sufficiently large to start laser action.

Various tricks can be used to obtain the atoms in state m. There may be higher levels to which the atoms can get if we shine in a strong beam of light of high frequency. From these high levels, they may trickle down, emitting various photons, until they all get stuck in the state m. If they tend to stay in the state m without emitting, the state is called metastable. And then they are all dumped down together by induced emissions. One more technical point—if we put this system in an ordinary box, it would radiate in so many different directions spontaneously, compared with the induced effect, that we would still be in trouble. But we can enhance the induced effect, increase its efficiency, by putting nearly perfect mirrors on each side of the box, so that the light which is emitted gets another chance, and another chance, and another chance, to induce more emission. Although the mirrors are almost one hundred percent reflecting, there is a slight amount of transmission of the mirror, and a little light gets out. In the end, of course, from the conservation of energy, all the light goes out in a nice uniform straight direction which makes the strong light beams that are possible today with lasers.

____________________________________________________________
Margin

1- This is not the only way one can arrange to keep the numbers of atoms in the various levels constant, but it is the way it actually works. That every process must, in thermal equilibrium, be balanced by its exact opposite is called the principle of detailed balancing.