تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Birthday Problem
المؤلف:
Abramson, M. and Moser, W. O. J.
المصدر:
"More Birthday Surprises." Amer. Math. Monthly 77
الجزء والصفحة:
...
6-3-2021
3695
+
-
20
Birthday Problem
Consider the probability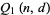 
that no two people out of a group of 
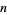will have matching birthdays out of 
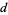equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person's birthday is different is 
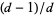, that the third person's birthday is different from the first two is ![[(d-1)/d][(d-2)/d]](https://mathworld.wolfram.com/images/equations/BirthdayProblem/Inline5.gif)
, and so on, up through the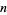 
th person. Explicitly,
 |
 |
 |
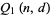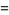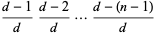(1) |
 |
 |
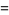![((d-1)(d-2)...[d-(n-1)])/(d^(n-1)).](https://mathworld.wolfram.com/images/equations/BirthdayProblem/Inline12.gif) |
(2) |
But this can be written in terms of factorials as
 |
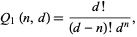(3) |
so the probability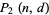 
that two or more people out of a group of 
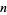do have the same birthday is therefore
 |
 |
 |
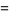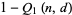(4) |
 |
 |
 |
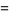(5) |
In general, let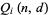 
denote the probability that a birthday is shared by exactly 
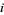(and no more) people out of a group of 
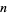people. Then the probability that a birthday is shared by 
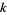or more people is given by
 |
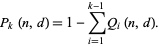(6) |
In general,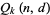 
can be computed using the recurrence relation
![Q_k(n,d)=sum_(i=1)^(|_n/k_|)[(n!d!)/(d^(ik)i!(k!)^i(n-ik)!(d-i)!)sum_(j=1)^(k-1)Q_j(n-ik,d-i)((d-i)^(n-ik))/(d^(n-ik))]](https://mathworld.wolfram.com/images/equations/BirthdayProblem/NumberedEquation3.gif) |
(7) |
(Finch 1997). However, the time to compute this recursive function grows exponentially with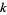 
and so rapidly becomes unwieldy.
If 365-day years have been assumed, i.e., the existence of leap days is ignored, and the distribution of birthdays is assumed to be uniform throughout the year (in actuality, there is a more than 6% increase from the average in September in the United States; Peterson 1998), then the number of people needed for there to be at least a 50% chance that at least two share birthdays is the smallest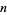 
such that 
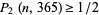. This is given by 
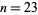, since
 |
 |
 |
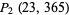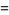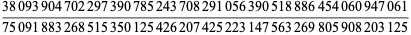(8) |
 |
 |
 |
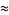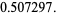(9) |
The number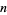 
of people needed to obtain 
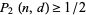for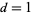 
, 2, ..., are 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, ... (OEIS A033810). The minimal number of people to give a 50% probability of having at least 
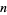coincident birthdays is 1, 23, 88, 187, 313, 460, 623, 798, 985, 1181, 1385, 1596, 1813, ... (OEIS A014088; Diaconis and Mosteller 1989).
The probability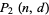 
can be estimated as
 |
 |
 |
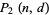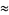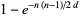(10) |
 |
 |
 |
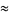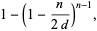(11) |
where the latter has error
 |
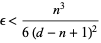(12) |
(Sayrafiezadeh 1994).
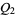can be computed explicitly as
 |
 |
 |
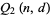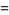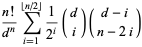(13) |
 |
 |
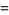![(d!)/(d^n(d-n)!)[_2F_1(1/2n,1/2(1-n);d-n+1;2)-1],](https://mathworld.wolfram.com/images/equations/BirthdayProblem/Inline53.gif) |
(14) |
where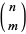 
is a binomial coefficient and 
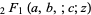is a hypergeometric function. This gives the explicit formula for 
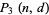as
 |
 |
 |
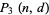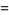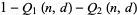(15) |
 |
 |
 |
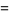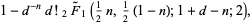(16) |
where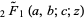 
is a regularized hypergeometric function.
A good approximation to the number of people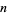 
such that 
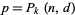is some given value can be given by solving the equation
![ne^(-n/(dk))=[d^(k-1)k!ln(1/(1-p))(1-n/(d(k+1)))]^(1/k)](https://mathworld.wolfram.com/images/equations/BirthdayProblem/NumberedEquation5.gif) |
(17) |
for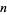 
and taking ![[n]](https://mathworld.wolfram.com/images/equations/BirthdayProblem/Inline67.gif)
, where ![[n]](https://mathworld.wolfram.com/images/equations/BirthdayProblem/Inline68.gif)
is the ceiling function (Diaconis and Mosteller 1989). For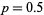 
and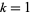 
, 2, 3, ..., this formula gives 
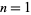, 23, 88, 187, 313, 459, 622, 797, 983, 1179, 1382, 1592, 1809, ... (OEIS A050255), which differ from the true values by from 0 to 4. A much simpler but also poorer approximation for 
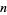such that 
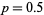for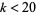 
is given by
 |
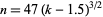(18) |
(Diaconis and Mosteller 1989), which gives 86, 185, 307, 448, 606, 778, 965, 1164, 1376, 1599, 1832, ... for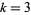 
, 4, ... (OEIS A050256).
The "almost" birthday problem, which asks the number of people needed such that two have a birthday within a day of each other, was considered by Abramson and Moser (1970), who showed that 14 people suffice. An approximation for the minimum number of people needed to get a 50-50 chance that two have a match within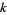 
days out of 
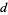possible is given by
 |
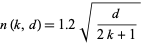(19) |
(Sevast'yanov 1972, Diaconis and Mosteller 1989).
REFERENCES:
Abramson, M. and Moser, W. O. J. "More Birthday Surprises." Amer. Math. Monthly 77, 856-858, 1970.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 45-46, 1987.
Bloom, D. M. "A Birthday Problem." Amer. Math. Monthly 80, 1141-1142, 1973.
Bogomolny, A. "Coincidence." http://www.cut-the-knot.org/do_you_know/coincidence.shtml.
Clevenson, M. L. and Watkins, W. "Majorization and the Birthday Inequality." Math. Mag. 64, 183-188, 1991.
Diaconis, P. and Mosteller, F. "Methods for Studying Coincidences." J. Amer. Statist. Assoc. 84, 853-861, 1989.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 31-32, 1968.
Finch, S. "Puzzle #28 [June 1997]: Coincident Birthdays." http://www.mathcad.com/library/LibraryContent/puzzles/puzzle.asp?num=28.
Gehan, E. A. "Note on the 'Birthday Problem.' " Amer. Stat. 22, 28, Apr. 1968.
Heuer, G. A. "Estimation in a Certain Probability Problem." Amer. Math. Monthly 66, 704-706, 1959.
Hocking, R. L. and Schwertman, N. C. "An Extension of the Birthday Problem to Exactly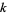 
Matches." College Math. J. 17, 315-321, 1986.
Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 102-103, 1975.
Klamkin, M. S. and Newman, D. J. "Extensions of the Birthday Surprise." J. Combin. Th. 3, 279-282, 1967.
Levin, B. "A Representation for Multinomial Cumulative Distribution Functions." Ann. Statistics 9, 1123-1126, 1981.
McKinney, E. H. "Generalized Birthday Problem." Amer. Math. Monthly 73, 385-387, 1966.
Mises, R. von. "Über Aufteilungs--und Besetzungs-Wahrscheinlichkeiten." Revue de la Faculté des Sciences de l'Université d'Istanbul, N. S. 4, 145-163, 1939. Reprinted in Selected Papers of Richard von Mises, Vol. 2 (Ed. P. Frank, S. Goldstein, M. Kac, W. Prager, G. Szegö, and G. Birkhoff). Providence, RI: Amer. Math. Soc., pp. 313-334, 1964.
Peterson, I. "MathTrek: Birthday Surprises." Nov. 21, 1998. http://www.sciencenews.org/sn_arc98/11_21_98/mathland.htm.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 179-180, 1994.
Sayrafiezadeh, M. "The Birthday Problem Revisited." Math. Mag. 67, 220-223, 1994.
Sevast'yanov, B. A. "Poisson Limit Law for a Scheme of Sums of Dependent Random Variables." Th. Prob. Appl. 17, 695-699, 1972.
Sloane, N. J. A. Sequences A014088, A033810, A050255, and A050256 in "The On-Line Encyclopedia of Integer Sequences."
Stewart, I. "What a Coincidence!" Sci. Amer. 278, 95-96, June 1998.
Tesler, L. "Not a Coincidence!" http://www.nomodes.com/coincidence.html.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
