


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-1-2021
Date: 6-9-2020
Date: 26-1-2020
|
A Liouville number is a transcendental number which has very close rational number approximations. An irrational number 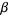 is called a Liouville number if, for each
is called a Liouville number if, for each 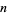 , there exist integers
, there exist integers 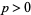 and
and 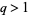 such that
such that
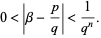 |
Note that the first inequality is true by definition, since it follows immediately from the fact that 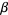 is irrational and hence cannot be equal to
is irrational and hence cannot be equal to 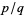 for any values of
for any values of 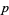 and
and 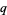 .
.
Liouville's constant is an example of a Liouville number and is sometimes called "the" Liouville number or "Liouville's number" (Wells 1986, p. 26). Mahler (1953) proved that 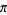 is not a Liouville number.
is not a Liouville number.
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 147, 1997.
Mahler, K. "On the Approximation of 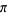 ." Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.
." Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|