تاريخ الفيزياء
علماء الفيزياء
الفيزياء الكلاسيكية
الميكانيك
الديناميكا الحرارية
الكهربائية والمغناطيسية
الكهربائية
المغناطيسية
الكهرومغناطيسية
علم البصريات
تاريخ علم البصريات
الضوء
مواضيع عامة في علم البصريات
الصوت
الفيزياء الحديثة
النظرية النسبية
النظرية النسبية الخاصة
النظرية النسبية العامة
مواضيع عامة في النظرية النسبية
ميكانيكا الكم
الفيزياء الذرية
الفيزياء الجزيئية
الفيزياء النووية
مواضيع عامة في الفيزياء النووية
النشاط الاشعاعي
فيزياء الحالة الصلبة
الموصلات
أشباه الموصلات
العوازل
مواضيع عامة في الفيزياء الصلبة
فيزياء الجوامد
الليزر
أنواع الليزر
بعض تطبيقات الليزر
مواضيع عامة في الليزر
علم الفلك
تاريخ وعلماء علم الفلك
الثقوب السوداء
المجموعة الشمسية
الشمس
كوكب عطارد
كوكب الزهرة
كوكب الأرض
كوكب المريخ
كوكب المشتري
كوكب زحل
كوكب أورانوس
كوكب نبتون
كوكب بلوتو
القمر
كواكب ومواضيع اخرى
مواضيع عامة في علم الفلك
النجوم
البلازما
الألكترونيات
خواص المادة
الطاقة البديلة
الطاقة الشمسية
مواضيع عامة في الطاقة البديلة
المد والجزر
فيزياء الجسيمات
الفيزياء والعلوم الأخرى
الفيزياء الكيميائية
الفيزياء الرياضية
الفيزياء الحيوية
الفيزياء العامة
مواضيع عامة في الفيزياء
تجارب فيزيائية
مصطلحات وتعاريف فيزيائية
وحدات القياس الفيزيائية
طرائف الفيزياء
مواضيع اخرى
جهد مورس Morse Potential
المؤلف:
الدكتور صلاح الدين محمود يونس
المصدر:
الفيزياء الجزيئية
الجزء والصفحة:
104
13-12-2020
3154
+
-
20
جهد مورس Morse Potential
عند دراسة المتذبذب التوافقي كتمثيل لاهتزاز جزيئة نلاحظ ان الجزيئة سوف لن تتفكك ابدا وفقا لهذا النموذج (انظر شكل 1) بينما جهد مورس يكون اسهل في تمثيل الجهد بين نواتين لجزيئة ثنائية الذرة وهو تقريب افضل للتركيب الاهتزازي للجزيئة من المتذبذب التوافقي لانه يتضمن صراحة تاثيرات كسر الآصرة وتفكك الجزيئة بالاضافة الى لاخطية الاواصر الحقيقية وفي شكل (1) نجد مقارنة بين جهد مورس والجهد التوافقي وعلى المحور العمودي طاقة الجهد بوحدات Eb وعلى المحور الافقي طول الاصرة بوحدات (a (r-re.
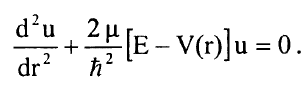........(i)
ان جهد مورس نموذج ملائم لجزيئة ثنائية الذرة كونه يسمح بحل دقيق لمعادلة شرودنجر (i)، وقد اقترح فيليب مورس الجهد بالصيغة:
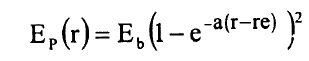.........(1)
حيث الثابت a يتحكم بعرض بئر الجهد ويعطي جهد مورس تقريب جيد لجزء التجاذب من الجهد الجزيئي بينما جزء التنافر منه يختلف عن القيم التجريبية كثيرا في عدة حالات.
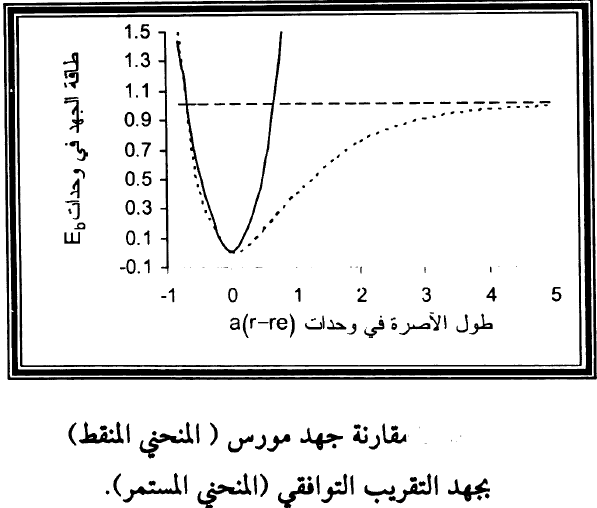
الشكل (1)
بإدخال المعادلة (1) في المعادلة (i) نحصل للطاقات (E(v على العلاقة:
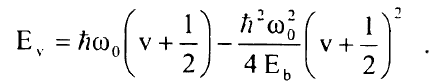.................(2)
ولقيم الحد الطيفي الاهتزازي 
بوحدات cm-1 نحصل على التعبير:
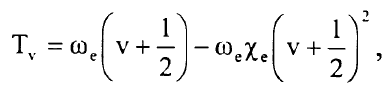................(3)
حيث يعود التردد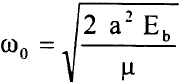 
لتردد المتذبذب الكلاسيكي ويمكن الحصول على الثابت a في جهد مورس من قياس ω0 وEb تعطى الفروق بين مستويات الطاقة الاهتزازي المتجاورة بوحدات cm-1 بالعلاقة:
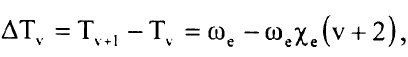..............(4)
وهي تقل خطيا مع العدد الكمي الاهتزازي v على التباين من المتذبذب التوافقي حيث الفروق ثابتة.
الاكثر قراءة في الفيزياء الجزيئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
مواضيع ذات صلة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
