Sort-Then-Add Sequence

The sequence produced by sorting the digits of a number and adding them to the previous number. The values starting with 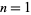, 2, ... are 2, 4, 6, 8, 10, 12, 14, 16, 18, 11, 22, 24, ... (OEIS A070196).

If the sorting-then-adding algorithm is applied iteratively until a sorted number is obtained, then for 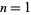, 2, ..., the algorithm terminates on 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 33, ... (OEIS A033862). The first few numbers not known to terminate are 316, 452, 697, 1376, 2743, 5090, ... (OEIS A033861). The least numbers of sort-then-add persistence 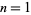, 2, ..., are 1, 10, 65, 64, 175, 98, 240, 325, 302, 387, 198, 180, 550, ... (OEIS A033863).

REFERENCES:

Sloane, N. J. A. Sequences A033861, A033862, A033863, and A070196 in "The On-Line Encyclopedia of Integer Sequences."a