Colour indices
 

The earlier simple discussion on black body radiation showed that the emitted energy from a star has a wavelength dependence according to its temperature. By applying Wien’s law, the temperature of a body could be obtained by measuring the wavelength at which the energy received has a maximum value. However, many of the stars are so hot as to place the energy peak somewhere in the ultraviolet region, beyond the position which can be investigated at the bottom of the Earth’s atmosphere. A more flexible technique involves temperature determination by measuring the ratio of received fluxes at two different wavelength positions on the energy–wavelength curve. This is illustrated in figure 1 by the black body curves depicted for two temperatures. It is obvious from an inspection of this figure that

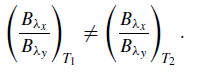
Figure 1. The black body curves for two temperatures.
It is, therefore, possible to express the ratio of energies received at two different wavelengths in the

where f (T ) is a known function that can be derived from the Planck formula describing the black body curve.
By using equation (15.13), the recorded magnitudes corresponding to these fluxes may be written

and

where k_λx and kλy are the appropriate constants giving the zero points for the two different magnitude scales. Therefore,
 (1)
The difference in magnitude m_λx− m_λy is known as the colour index of the star and its determination leads to an assessment of the star’s effective temperature. In practice, many different bandpass systems corresponding to λ_x and λ_y are used. A colour index system can be applied to any pair of such magnitude scales with the difference in the values of the constants k_λx−k_λy being chosen to be zero for some particular temperature. Thus, colour indices may be derived from photographic magnitude measurements—m_pg, m_pv. More modern systems are based on UBV magnitudes and are usually written as B−V and U −B. Table 1 shows how the colour index defined by B−V depends on the surface temperature of the star.
A note of caution is perhaps due here in respect of the ‘signs’ of the values of colour indices. Suppose that in figure 1 the wavelengths λx and λy correspond to B and V respectively. For the lower temperature (T₂), the flux at B is lower than at V. A quick assessment might suggest that B −V would be negative. However, the values of B and V are expressed in magnitudes which carry an inverse scale and hence B − V is, in fact, positive. For objects with higher temperature (T₁), the flux at B is

Table1. Colour index as a function of temperature (main sequence stars).

greater than at V and, hence, B − V (measured as a magnitude difference) is negative. The higher the temperature, the more negative B − V becomes.
If theoretical black body curves are used to represent the radiation from stars, the B − V colour index can be expressed to a good approximation as
 (2)
Using equation 2, temperatures may be estimated from measurements of the B − V colour index. In practice, the expression needs modification to allow for the fact that stars do not behave as perfect black bodies and care must also be taken for the effects that absorption by interstellar material can have on the apparent colours of stars.