Proof of the four-parts formula
المؤلف:
A. Roy, D. Clarke
المصدر:
Astronomy - Principles and Practice 4th ed
الجزء والصفحة:
P 55
20-7-2020
2182
Proof of the four-parts formula
Let the four consecutive parts be B, a, C and b. Then side a, between the angles, is the ‘inner side’, b being the ‘other’; angle C, between sides a and b, is the ‘inner angle’ with B the ‘other’. We want to prove that
cos a cosC = sin a cot b − sin C cot B.
From the cosine formulas (1) ,
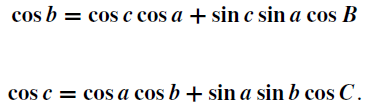..............(1)
we have
cos b = cos c cos a + sin c sin a cos B (2)
cos c = cos a cos b + sin a sin b cosC. (3)
Substituting the right-hand side of equation (3) for cos c in equation (2), we obtain
cos b(1 − cos2 a) = cos a sin a sin b cosC + sin c sin a cos B.
Substituting sin2 a for (1 − cos2 a) and dividing throughout by sin a sin b, we get
cot b sin a = cos a cosC + sin c/sin b cos B. (4)
Using the sine formula (7.7) it is seen that
.
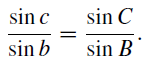
Hence, equation (4) becomes
cos a cosC = sin a cot b − sin C cot B.
الاكثر قراءة في مواضيع عامة في علم الفلك
اخر الاخبار
اخبار العتبة العباسية المقدسة
