Elliptic Exponential Function
المؤلف:
Wolfram, S.
المصدر:
The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media
الجزء والصفحة:
p. 788
8-7-2020
1528
Elliptic Exponential Function
The elliptic exponential function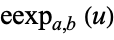 
gives the value of 
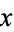in the elliptic logarithm
for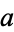 
and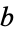 
real such that 
.
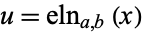It is implemented in the Wolfram Language as EllipticExp[u, ![<span style=]()
{" src="https://mathworld.wolfram.com/images/equations/EllipticExponentialFunction/Inline6.gif" style="height:15px; width:5px" />a, b![<span style=]()
}" src="https://mathworld.wolfram.com/images/equations/EllipticExponentialFunction/Inline7.gif" style="height:15px; width:5px" />], which returns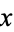 
together with the superfluous parameter 
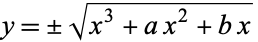which multiplies the above integral by a factor of 
.
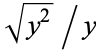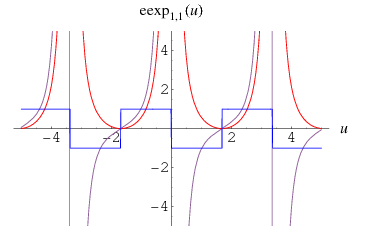
The top plot above shows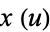 
(red), 
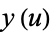(violet), and 
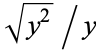(blue) for 
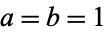. The other plots show 
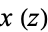in the complex plane.
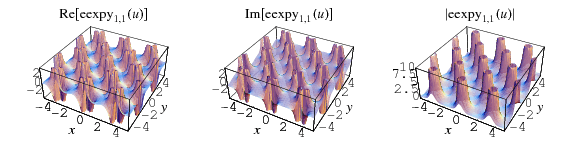
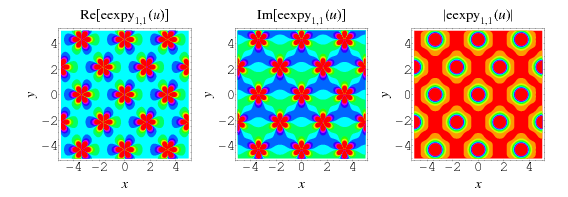
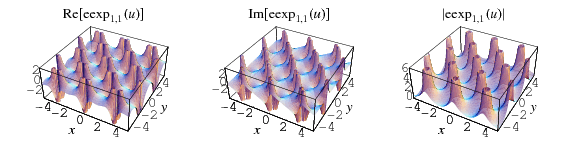
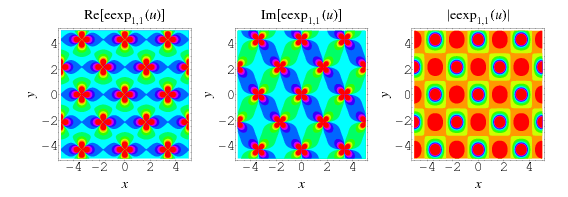
The plots above show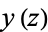 
in the complex plane for 
.
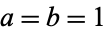As can be seen from the plots, the elliptic exponential function is doubly periodic in the complex plane.
REFERENCES:
Wolfram, S. The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media, p. 788, 2003.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
