Sphere Packing

Define the packing density 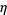 of a packing of spheres to be the fraction of a volume filled by the spheres. In three dimensions, there are three periodic packings for identical spheres: cubic lattice, face-centered cubic lattice, and hexagonal lattice. It was hypothesized by Kepler in 1611 that close packing (cubic or hexagonal, which have equivalent packing densities) is the densest possible, and this assertion is known as the Kepler conjecture. The problem of finding the densest packing of spheres (not necessarily periodic) is therefore known as the Kepler problem, where

(OEIS A093825; Steinhaus 1999, p. 202; Wells 1986, p. 29; Wells 1991, p. 237).

In 1831, Gauss managed to prove that the face-centered cubic is the densest lattice packing in three dimensions (Conway and Sloane 1993, p. 9), but the general conjecture remained open for many decades.

While the Kepler conjecture is intuitively obvious, the proof remained surprisingly elusive. Rogers (1958), a well-known researcher on the problem, remarked that "many mathematicians believe, and all physicists know" that the actual answer is 74.048% (Conway and Sloane 1993, p. 3). For packings in three dimensions, C. A. Rogers (1958) showed that the maximum possible packing density 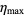 satisfies

(Le Lionnais 1983), and this result was subsequently improved to 77.844% (Lindsey 1986), then 77.836% (Muder 1988). A proof of the full conjecture was finally accomplished in a series of papers by Hales culminating in 1998.

Interestingly, the packing density in ellipsoid packing can exceed .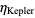

The maximum number of equivalent spheres (or 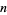-dimensional hyperspheres) which can touch an equivalent sphere (hypersphere) without intersections is called the 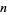-dimensional kissing number.

The packing densities for several types of sphere packings are summarized in the following table. In a 1972 personal communication to Martin Gardner, Ulam conjectured that in their densest packing, spheres allow more empty space than the densest packing of any other identical convex solids (Gardner 2001, p. 135).

packing	analytic	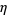	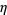reference
loosest possible	--	0.0555	Gardner (1966)
tetrahedral lattice		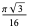0.3401	Hilbert and Cohn-Vossen (1999, pp. 48-50)
cubic lattice		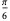0.5236
hexagonal lattice		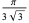0.6046
random	--	0.6400	Jaeger and Nagel (1992)
face-centered cubic close packing		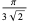0.7405	Steinhaus (1999, p. 202), Wells (1986, p. 29; 1991, p. 237)
body-centered cubic close packing		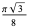0.6801
hexagonal close packing		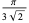0.7405	Steinhaus (1999, p. 202), Wells (1986, p. 29; 1991, p. 237)

The rigid packing with lowest density known has 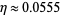 (Gardner 1966), significantly lower than that reported by Hilbert and Cohn-Vossen (1999, p. 51). To be rigid, each sphere must touch at least four others, and the four contact points cannot be in a single hemisphere or all on one equator.

Hilbert and Cohn-Vossen (1999, pp. 48-50) consider a tetrahedral lattice packing in which each sphere touches four neighbors and the density is 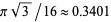. This is the lattice formed by carbon atoms in a diamond (Conway and Sloane 1993, p. 113).

Random close packing of spheres in three dimensions gives packing densities in the range 0.06 to 0.65 (Jaeger and Nagel 1992, Torquato et al. 2000). Compressing a random packing gives polyhedra with an average of 13.3 faces (Coxeter 1958, 1961).

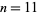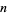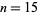For sphere packing inside a cube, see Goldberg (1971), Schaer (1966), Gensane (2004), and Friedman. The results of Gensane (2004) improve those of Goldberg for , 12, and all  from  to 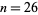 except for  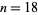and are almost certainly optimal.

REFERENCES:

Barlow, W. "Probable Nature of the Internal Symmetry of Crystals." Nature 29, 186-188, 1883.

Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, 1993.

Coxeter, H. S. M. "Close-Packing and so Forth." Illinois J. Math. 2, 746-758, 1958.

Coxeter, H. S. M. "Close Packing of Equal Spheres." Section 22.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 405-411, 1961.

Coxeter, H. S. M. "The Problem of Packing a Number of Equal Nonoverlapping Circles on a Sphere." Trans. New York Acad. Sci. 24, 320-331, 1962.

Critchlow, K. Order in Space: A Design Source Book. New York: Viking Press, 1970.

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 195-197, 1989.

Eppstein, D. "Covering and Packing." http://www.ics.uci.edu/~eppstein/junkyard/cover.html.

Fejes Tóth, G. "Über einen geometrischen Satz." Math. Z. 46, 78-83, 1940.

Fejes Tóth, G. Lagerungen in der Ebene, auf der Kugel und in Raum, 2nd ed. Berlin: Springer-Verlag, 1972.

Friedman, E. "Spheres in Cubes." http://www.stetson.edu/~efriedma/sphincub/.

Gardner, M. "Packing Spheres." Ch. 7 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, pp. 82-90, 1966.

Gardner, M. "Packing Spheres." Ch. 10 in The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. New York: W. W. Norton, pp. 128-136, 2001.

Gauss, C. F. "Besprechung des Buchs von L. A. Seeber: Intersuchungen über die Eigenschaften der positiven ternären quadratischen Formen usw." Göttingsche Gelehrte Anzeigen (1831, July 9) 2, 188-196, 1876.

Gensane, T. "Dense Packings of Equal Spheres in a Cube." Electronic J. Combinatorics 11, No. 1, R33, 2004. http://www.combinatorics.org/Volume_11/PDF/v11i1r33.pdf.

Goldberg, M. "On the Densest Packing of Equal Spheres in a Cube." Math. Mag. 44, 199-208, 1971.

Hales, T. C. "The Sphere Packing Problem." J. Comput. Appl. Math 44, 41-76, 1992.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, pp. 45-53, 1999.

Jaeger, H. M. and Nagel, S. R. "Physics of Granular States." Science 255, 1524, 1992.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 31, 1983.

Lindsey, J. H. II. "Sphere Packing in 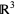." Math. 33, 137-147, 1986.

Muder, D. J. "Putting the Best Face of a Voronoi Polyhedron." Proc. London Math. Soc. 56, 329-348, 1988.

Rogers, C. A. "The Packing of Equal Spheres." Proc. London Math. Soc. 8, 609-620, 1958.

Rogers, C. A. Packing and Covering. Cambridge, England: Cambridge University Press, 1964.

Schaer, J. "On the Densest Packing of Spheres in a Cube." Can. Math. Bul. 9, 265-270, 1966.

Sigrist, F. "Sphere Packing." Math. Intell. 5, 34-38, 1983.

Sloane, N. J. A. "The Packing of Spheres." Sci. Amer. 250, 116-125, 1984.

Sloane, N. J. A. "The Sphere Packing Problem." Proc. Internat. Congress Math., Vol. 3 (Berlin, 1998). Doc. Math. Extra Volume ICM 1998, 387-396, 1998. http://www.research.att.com/~njas/doc/icm.ps.

Sloane, N. J. A. Sequence A093825 in "The On-Line Encyclopedia of Integer Sequences."

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 202-203, 1999.

Stewart, I. The Problems of Mathematics, 2nd ed. Oxford, England: Oxford University Press, pp. 69-82, 1987.

Thompson, T. M. From Error-Correcting Codes Through Sphere Packings to Simple Groups. Washington, DC: Math. Assoc. Amer., 1984.

Torquato, S.; Truskett, T. M.; and Debenedetti, P. G. "Is Random Close Packing of Spheres Well Defined?" Phys. Lev. Lett. 84, 2064-2067, 2000.

van Dam, E.; den Hertog, D.; Husslage, B.; and Rennen, G. "Maximin Designs (Dimensions: 3)." Mar. 31, 2006. http://www.spacefillingdesigns.nl/.

Weisstein, E. W. "Books about Sphere Packings." http://www.ericweisstein.com/encyclopedias/books/SpherePackings.html.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 29, 1986.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, 237-238, 1991.

Zong, C. and Talbot, J. Sphere Packings. New York: Springer-Verlag, 1999.