المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hh Function |
 1362
 01:54 صباحاً
date: 28-4-2019 |
Author : Jeffreys, H. and Jeffreys, B. S. 
Book or Source : "The Parabolic Cylinder, Hermite, and Hh Functions" et seq. §23.08-23.081 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge... 
Page and Part : pp. 620-627|
Read More
Date: 21-8-2019
1874
Date: 12-10-2018
1957
Date: 21-7-2019
1827
|
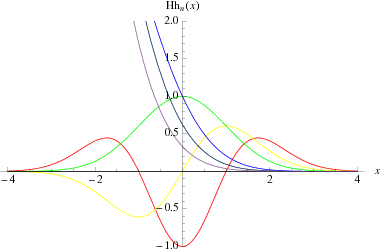
Let
 |
 |
 |
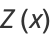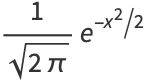(1) |
 |
 |
 |
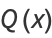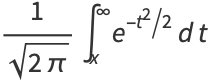(2) |
 |
 |
![1/2[1-erf(x/(sqrt(2)))],](http://mathworld.wolfram.com/images/equations/HhFunction/Inline9.gif) |
(3) |
where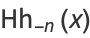 
and 
are closely related to the normal distribution function, then
 |
 |
 |
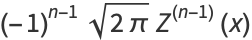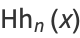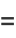(4) |
 |
 |
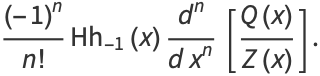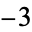![((-1)^n)/(n!)Hh_(-1)(x)(d^n)/(dx^n)[(Q(x))/(Z(x))].](http://mathworld.wolfram.com/images/equations/HhFunction/Inline17.gif) |
(5) |
The first few values are
 |
 |
 |
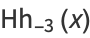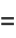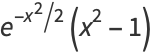(6) |
 |
 |
 |
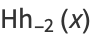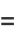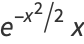(7) |
 |
 |
 |
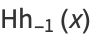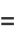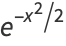(8) |
 |
 |
 |
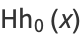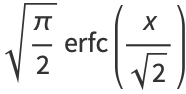(9) |
 |
 |
 |
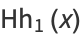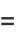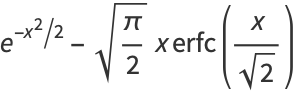(10) |
 |
 |
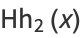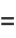![1/4[-2xe^(-x^2/2)+sqrt(2pi)(x^2+1)erfc(x/(sqrt(2)))]](http://mathworld.wolfram.com/images/equations/HhFunction/Inline35.gif) |
(11) |
 |
 |
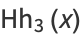![1/(12)[2e^(-x^2/2)(x^2+2)-sqrt(2pi)x(x^2+3)erfc(x/(sqrt(2)))].](http://mathworld.wolfram.com/images/equations/HhFunction/Inline38.gif) |
(12) |
REFERENCES:
Jeffreys, H. and Jeffreys, B. S. "The Parabolic Cylinder, Hermite, and Hh Functions" et seq. §23.08-23.081 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 620-627, 1988.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|
