
Green,s Function--Poisson,s Equation
 المؤلف:
Arfken, G
المؤلف:
Arfken, G
 المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
 الجزء والصفحة:
pp. 485-486, 905, and 912
الجزء والصفحة:
pp. 485-486, 905, and 912
 26-12-2018
26-12-2018
 977
977
Green's Function--Poisson's Equation
Poisson's equation is
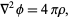 |
(1)
|
where 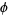 is often called a potential function and
is often called a potential function and 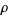 a density function, so the differential operator in this case is
a density function, so the differential operator in this case is 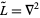 . As usual, we are looking for a Green's function
. As usual, we are looking for a Green's function 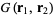 such that
such that
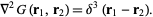 |
(2)
|
But from Laplacian,
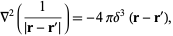 |
(3)
|
so
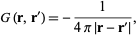 |
(4)
|
and the solution is
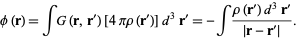 |
(5)
|
Expanding 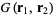 in the spherical harmonics
in the spherical harmonics 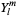 gives
gives
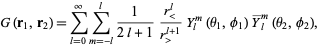 |
(6)
|
where  and
and 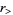 are greater than/less than symbols. this expression simplifies to
are greater than/less than symbols. this expression simplifies to
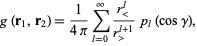 |
(7)
|
where 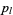 are Legendre polynomials, and
are Legendre polynomials, and 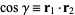 . Equations (6) and (7) give the addition theorem for Legendre polynomials.
. Equations (6) and (7) give the addition theorem for Legendre polynomials.
In cylindrical coordinates, the Green's function is much more complicated,
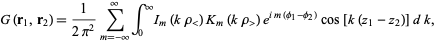 |
(8)
|
where 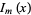 and
and 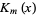 are modified Bessel functions of the first and second kinds (Arfken 1985).
are modified Bessel functions of the first and second kinds (Arfken 1985).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 485-486, 905, and 912, 1985.
 الاكثر قراءة في معادلات تفاضلية
الاكثر قراءة في معادلات تفاضلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


