


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 12-7-2018
Date: 12-7-2018
|
For the hyperbolic partial differential equation
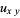 |
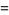 |
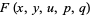 |
(1) |
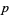 |
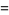 |
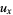 |
(2) |
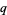 |
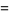 |
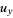 |
(3) |
on a domain 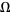 , Goursat's problem asks to find a solution
, Goursat's problem asks to find a solution 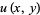 of (3) from the boundary conditions
of (3) from the boundary conditions
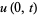 |
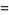 |
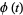 |
(4) |
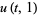 |
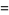 |
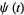 |
(5) |
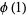 |
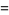 |
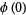 |
(6) |
for 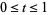 that is regular in
that is regular in 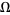 and continuous in the closure
and continuous in the closure 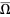 , where
, where 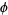 and
and 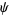 are specified continuously differentiable functions.
are specified continuously differentiable functions.
The linear Goursat problem corresponds to the solution of the equation
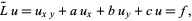 |
(7) |
which can be effected using the so-called Riemann function 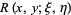 . The use of the Riemann function to solve the linear Goursat problem is called the Riemann method.
. The use of the Riemann function to solve the linear Goursat problem is called the Riemann method.
REFERENCES:
Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 2. New York: Wiley, 1989.
Goursat, E. A Course in Mathematical Analysis, Vol. 3: Variation of Solutions and Partial Differential Equations of the Second Order & Integral Equations and Calculus of Variations Paris: Gauthier-Villars, 1923.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, p. 289, 1988.
Tricomi, F. G. Integral Equations. New York: Interscience, 1957.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|