
Solving Systems of Inequalities
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
www.almerja.com
المصدر:
www.almerja.com
 الجزء والصفحة:
...
الجزء والصفحة:
...
 8-3-2017
8-3-2017
 1781
1781
We first need to learn the symbols for inequalities:
The symbol < means less than.
The symbol > means greater than.
The symbol < with a bar underneath means less than or equal to. Usually this is written as <= on computers because it is simple to write and understand.
The symbol > with a bar underneath means greater than or equal to. Usually this is written as >= on computers because it is simple to write and understand.
There are endless solutions for inequalities. In light of this fact, it is best to find a solution set for inequalities by solving the system graphically.
How To Solve Systems of Inequalities Graphically:
1) Write the inequality in slope-intercept form or in the form y = mx + b.
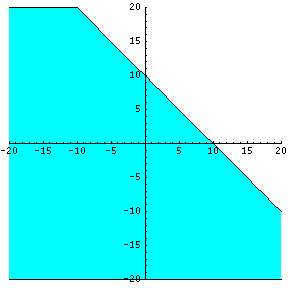
Sample A: Solve x + y <=10.
Firstly, x + y < = 10 becomes y <= -x + 10.
2) Temporarily exchange the given inequality symbol (in this case <=) for the equal symbol. In doing so, you can treat the inequality like an equation. BUT DO NOT forget to replace the equal symbol with the original inequality symbol at the END of the problem.
So, y <= -x + 10 becomes y = -x + 10.
3) Plug different values for x to find points that will be graphed in the form (x,y).
When x = 1, y = 9
When x = 0, y = 10
When x = 4, y = 6
When x = 6, y = 4
The following points will be graphed on the xy-plane:
(1,9), (0,10), (4,6) and (6,4)
NOTE:
Points ABOVE the graph line represent all points where
y > -x + 10. Points BELOW the graph line (shaded) represent all points where y < -x + 10.
For our Sample A question, y <= -x + 10, all points on or below the graph line satisfy the original inequality. This means that if you were to select points on or below the graph line and plug those points into the original inequality, the inequality will reveal a TRUE statement. I will try one and you can look for more points if you'd like.
I will plug point (-2,2) into the original inequality to test if point (-2,2) will yield a true statement.
Our original inequality is:
x + y <= 10.
(-2) + (2) <= 10
0 <= 10 is a TRUE statement.
Thus, we now know that every point below the graph line will satisfy the inequality. You may select any point on this graph line for further testing if you'd like.
Sample B: Solve y >= -3/2x + 6
Notice that this inequality is already in the slope-intercept form.
I will replace the given inequality symbol for the equal symbol.
So, y >= -3/2x + 6 becomes y = -3/2x + 6.
I will now plug different values for x to find y and thus create points in the form (x,y).
When x = 1, y = 4.5
When x = 2, y = 3
When x = 3, y = 1.5
When x = 4, y = 0
Our points to be graphed:
(1,4.5), (2,3), (3,1.5) and (4,0)
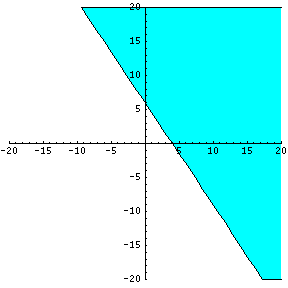
After applying basic algebra, we learn that all points on or ABOVE this graph line will satisfy our second original inequality. Again, I will select any point above the graph line to make sure that it will satisfy or reveal a TRUE statement in terms of the original inequality in our Sample B.
I will use point (5,3).
Our original inequality is:
y >= -3/2x + 6
3 >= -3/2(5) + 6
3 >= -1.5. This is a TRUE statement and thus, point (5,3), which is above the graph line, satisfies our original inequality.

 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


