
How To Find The Limit
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
www.almerja.com
المصدر:
www.almerja.com
 الجزء والصفحة:
...
الجزء والصفحة:
...
 6-3-2017
6-3-2017
 1727
1727
A limit is a certain value to which a function approaches. Finding a limit means finding what value y is as x approaches a certain number. You would typical say that the limit of a certain function is <a number> as x approaches <some x coordinate>. For example, imagine a curve such that as x approaches infinity, that curve may come closer and closer to y=0 while never actually getting there. So, how do we algebraically find that limit? One way to find the limit is by theSUBSTITUTION METHOD.
For example, the limit of the following graph is 0 as x approaches infinity, because the graph approaches 0:
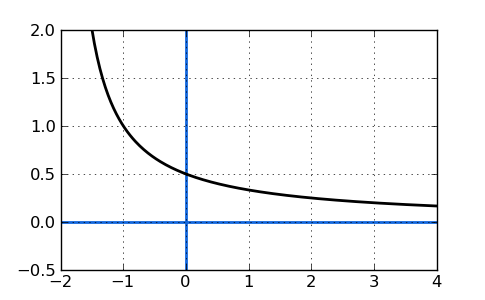
Now, let's look at a few examples where we can find the limit of real functions:
Sample A: Find the limit of f(x) = 4x, as x approaches 3.
Steps:
1) Replace x for 3.
2) Simplify.
f(x) = 4x becomes f(3) = 4(3) = 12.
So, the limit of f(x) = 4x as x approaches 3 is 12.
In this case the solution was straightforward, because the function not only "approaches" 12 but goes right through it!
Sample B: Find the limit:
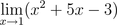
Follow the same steps as above.
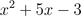
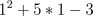
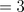
So, the limit of x^2 + 5x - 3 as x approaches 1 is 3.
However, the substitution method will not always work. For Sample C below, you must factor the numerator first BEFORE applying the substitution method.
Sample C:

If we substitute 0 for x in Sample C, we will create division by zero which DOES NOT EXIST or is UNDEFINED. This is the reason factoring MUST be our first step in this sample.
Factoring the numerator for x, which is common to both terms, gives us:
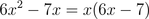
We can now cancel x in the numerator and denominator. When we cancel BOTH variables x, we are left with:
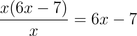
Now, we can substitute 0 for x in 6x - 7 to find the limit is -7:
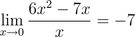
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


