In simpler terms, that means if A is always twice as much as B, then they directly vary. If a gallon of milk costs $2, and I buy 1 gallon, the total cost is $2. If I buy 10 gallons, the price is $20. In this example the total cost of milk and the number of gallons purchased are subject to direct variation -- the ratio of the cost to the number of gallons is always 2.

To be more "mathematical" about it, if y varies directly as x, then the graph of all points that describe this relationship is a line going through the origin (0, 0) whose slope is called the constant of the variation. That's because each of the variables is a constant multiple of the other, like in the graph shown below:

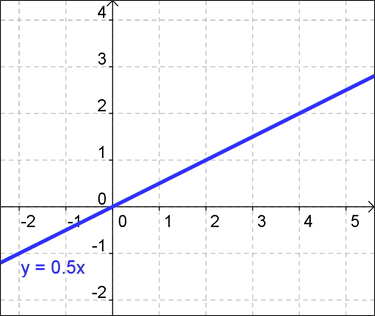
Let's review several key concepts of direct variation:

1) Expressing Direct Variation as an Equation

The equation y/x = 6 states that y "varies directly as" x since the ratio of y to x (also written y:x) never changes. The number 6 in the equation y/x = 6 is called the constant of variation. The equation y/x = 6 can also be written in the equivalent form, y = 6x. That form shows you that y is always 6 times as much as x.

Similarly, for the equation y=x/3, the constant of variation is 1/3. The equation tells us that for any x value, y will always be 1/3 as much.

2) Algebraic Interpretation of Direct Variation

For an equation of the form y = kx, multiplying x by some fixed amount also multiplies y by the SAME FIXED AMOUNT. If we double x, then we also double the corresponding y value. What does this mean? For example, since the perimeter P of a square varies directly as the length of one side of a square, we can say that P = 4s, where the number 4 represents the four sides of a square and s represents the length of one side. That equation tells us that the perimeter is always four times the length of a single side (makes sense, right?), but it also tells us that doubling the length of a side doubles the perimeter (which will still be four times larger in total).

3) Geometric Interpretation of Direct Variation

The equation y = kx is a special case of linear equation (y=mx+b) where the y-intercept equals 0. (Note: the equation y = mx + b is the slope-intercept form where m is the slope and b is the y-intercept). Anyway, a straight line through the origin (0,0) always represents a direct variation between y and x. The slope of this line is the constant of variation. In other words, in the equation y = mx + b, m is the constant of variation.

Example A:

If y varies directly as x, and y = 8 when x = 12, find k and write an equation that expresses this variation.

Plan of Attack:

Plug the given values into the equation y = kx.

Solve for k.

Then replace k with its value in the equation y = kx.

Step-by-Step:

Start with our standard equation: y = kx

Insert our known values: 8 = k*12

Divide both sides by 12 to find k: 8/12 = k

2/3 = k

Next: Go back to y = kx and replace k with 2/3.

Result:

y = (2/3)x

Example B:

If y varies directly as x, and y = 24 when x = 16, find y when x = 12.

Plan of Attack:

When two quantities vary directly, their ratio is always the same. We'll create two ratios, set them equal to each other, and then solve for the missing quantity.

Step-by-Step:

The given numbers form one ratio expressed as y/x: (24/16)

To find y when x=12 we setup another ratio: (y/12)

Solve:

By definition, both ratios are equal: (24/16) = (y/12)

Multiply each side by 12 to solve for y: (1.5)*12=y

Result:

18 = y

مواضيع ذات صلة

Zero Set

Xi-Function

Weierstrass Product Theorem

Tangent

Tanc Function

Simple Root

Separation Theorem

Rouché,s Theorem

Root Linear Coefficient Theorem

Root

Multiplicity

Multiple Root