The Gibbs–Duhem equation
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص139-141
2025-11-12
199
The Gibbs–Duhem equation
Because the total Gibbs energy of a binary mixture is given by eqn 5.5 and the chemical potentials depend on the composition, when the compositions are changed infinitesimally we might expect G of a binary system to change by , dG=µAdnA+µBdnB+nAdµA+nBdµB , However, we have seen that at constant pressure and temperature a change in Gibbs energy is given by eqn 5.7. Because G is a state function, these two equations must be equal, which implies that at constant temperature and pressure , nAdµA +nBdµB=0 , This equation is a special case of the Gibbs–Duhem equation:
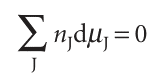
The significance of the Gibbs–Duhem equation is that the chemical potential of one component of a mixture cannot change independently of the chemical potentials of the other components. In a binary mixture, if one partial molar quantity increases, then the other must decrease, with the two changes related by
The same line of reasoning applies to all partial molar quantities. We can see in Fig. 5.1, for example, that, where the partial molar volume of water increases, that of ethanol decreases. Moreover, as eqn 5.13 shows, and as we can see from Fig. 5.1, a small change in the partial molar volume of A corresponds to a large change in the partial molar volume of B if nA/nB is large, but the opposite is true when this ratio is small. In practice, the Gibbs–Duhem equation is used to determine the partial molar volume of one component of a binary mixture from measurements of the partial molar volume of the second component.
Fig. 5.5 The partial molar volumes of the components of an aqueous solution of potassium sulfate.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
