The Clausius inequality
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص86-87
2025-11-05
267
The Clausius inequality
We now show that the definition of entropy is consistent with the Second Law. To begin, we recall that more energy flows as work under reversible conditions than under irreversible conditions. That is, −dwrev ≥−dw, or dw − dwrev ≥ 0. Because the internal energy is a state function, its change is the same for irreversible and reversible paths between the same two states, so we can also write: dU=dq+dw=dqrev+dwrev It follows that dqrev − dq = dw − dwrev ≥ 0, or dqrev ≥ dq, and therefore that dqrev/T ≥ dq/T. Now we use the thermodynamic definition of the entropy (eqn 3.1; dS = dqrev/T) to write
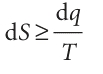
This expression is the Clausius inequality. It will prove to be of great importance for the discussion of the spontaneity of chemical reactions, as we shall see in Section 3.5.
We now suppose that the system is isolated from its surroundings, so that dq = 0. The Clausius inequality implies that dS ≥0 and we conclude that in an isolated system the entropy cannot decrease when a spontaneous change occurs. This statement captures the content of the Second Law.
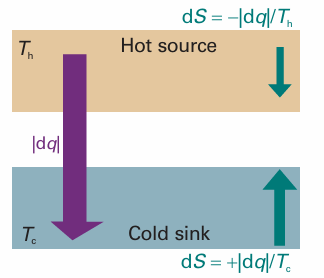
Fig. 3.11 When energy leaves a hot reservoir as heat, the entropy of the reservoir decreases. When the same quantity of energy enters a cooler reservoir, the entropy increases by a larger amount. Hence, overall there is an increase in entropy and the process is spontaneous. Relative changes in entropy are indicated by the sizes of the arrows.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
