The principle of corresponding states
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص21-22
2025-10-30
35
The principle of corresponding states
An important general technique in science for comparing the properties of objects is to choose a related fundamental property of the same kind and to set up a relative scale on that basis. We have seen that the critical constants are characteristic proper ties of gases, so it may be that a scale can be set up by using them as yardsticks. We therefore introduce the dimensionless reduced variables of a gas by dividing the actual variable by the corresponding critical constant:
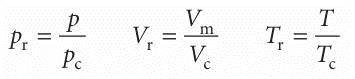
If the reduced pressure of a gas is given, we can easily calculate its actual pressure by using p=pr pc, and likewise for the volume and temperature. Van der Waals, who first tried this procedure, hoped that gases confined to the same reduced volume, Vr, at the same reduced temperature, Tr, would exert the same reduced pressure, pr. The hope was largely fulfilled (Fig. 1.19). The illustration shows the dependence of the com pression factor on the reduced pressure for a variety of gases at various reduced temperatures. The success of the procedure is strikingly clear: compare this graph with Fig. 1.14, where similar data are plotted without using reduced variables. The observation that real gases at the same reduced volume and reduced temperature exert the same reduced pressure is called the principle of corresponding states. The principle is only an approximation. It works best for gases composed of spherical molecules; it fails, sometimes badly, when the molecules are non-spherical or polar. The van der Waals equation sheds some light on the principle. First, we express eqn 1.21b in terms of the reduced variables, which gives
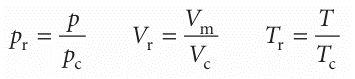
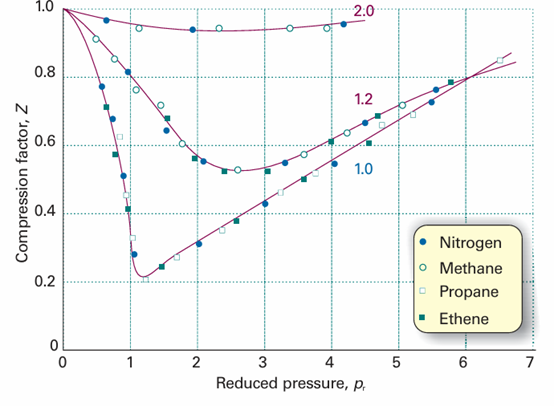
Fig. 1.19The compression factors of four of the gases shown in Fig. 1.14 plotted using reduced variables. The curves are labelled with the reduced temperature Tr=T/Tc. The use of reduced variables organizes the data on to single curves.
Exploration Is there a set of conditions at which the compression factor of a van der Waals gas passes through a minimum? If so, how does the location and value of the minimum value of Z depend on the coefficients a and b?
Then we express the critical constants in terms of a and b by using eqn 1.22:
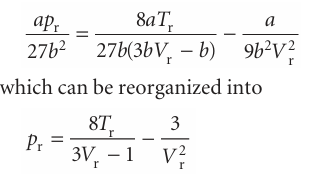
This equation has the same form as the original, but the coefficients a and b, which differ from gas to gas, have disappeared. It follows that if the isotherms are plotted in terms of the reduced variables (as we did in fact in Fig. 1.18 without drawing attention to the fact), then the same curves are obtained whatever the gas. This is precisely the content of the principle of corresponding states, so the van der Waals equation is compatible with it. Looking for too much significance in this apparent triumph is mistaken, because other equations of state also accommodate the principle (Table 1.7). In fact, all we need are two parameters playing the roles of a and b, for then the equation can always be manipulated into reduced form. The observation that real gases obey the principle approximately amounts to saying that the effects of the attractive and repulsive inter actions can each be approximated in terms of a single parameter. The importance of the principle is then not so much its theoretical interpretation but the way that it enables the properties of a range of gases to be coordinated on to a single diagram (for example, Fig. 1.19 instead of Fig. 1.14).
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
