Effect on the Lattice Parameter

Let us now consider the effects of the increase in the surface-to-volume ratio as the object size decreases. To do this, we consider first the very simple case of a liquid sphere of diameter 2R. Due to the curvature of the surface, a pressure is generated toward the inside of the sphere. The excess pressure ΔP inside the sphere, in the purely hydrostatic case, is given by the Laplace equation

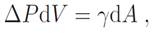                      (1)

where dV is the volume change corresponding to a change dA in the area of the droplet. In the case of a sphere, (above) takes the form

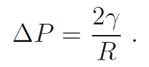                      (2)

For a spherical solid, the specific surface energy must be replaced by the surface stress tensor gij . To simplify the problem, consider the case of a solid with simple cubic structure. In this case, γ is isotropic and we have

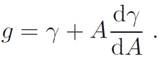                       (3)

Moreover, we may recall the definition of the compressibility, viz.,

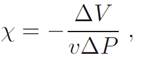                        (4)

where v is the atomic volume of the solid, which can also be defined as a3,  where a is the lattice parameter. Combining (1) and (4), We obtain the relative variation of the lattice parameter:

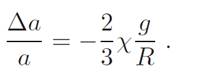
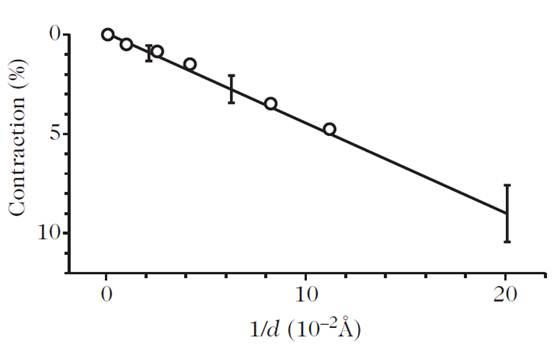
Fig. 1. Contraction of the lattice parameter of copper clusters as a function of the reciprocal of their diameter. Circles correspond to measurements of electron energy loss near an ionisation threshold (SEELFS). Taken from De Crescenzi et al. [1]. The straight line shows measurements of X-ray absorption (EXAFS). Taken from Apai et al. [2]

We thus find that there is a contraction of the crystal lattice due to the pressure exerted toward the interior of the particle. This contraction is proportional to the surface stress and inversely proportional to the particle size.

   The lattice contraction in nanometric particles has been observed on many occasions. Figure 1 shows the change in lattice parameter for copper clusters,  measured by the electron energy loss technique known as SEELFS andalso by X-ray absorption near an ionisation threshold (see below).

References

1. M. De Crescenzi, M. Diociaiuti, L. Lozzi, P. Picozzi, S. Santucci: Phys. Rev.  B35, 5997 (1987)

2. G. Apai, J.F. Hamilton, J. St¨ohr, A. Thomson: Phys. Rev. Lett.43, 165 (1979)

مواضيع ذات صلة

تشخيص فريت الكوبلت (CoFe2O4) النانوي بواسطة حيود الاشعة السينية

تشخيص فريت الكوبالت (CoFe2O4) النانوي بواسطة طيف الاشعة تحت الحمراء

فريت الكوبلت النانوي CoFe2O4

تحضير فريت الاسبنيل النانوية M=Co, Ni, Cu , Zn) MFe2O) بواسطة الكيمياء الخضراء

العلاج بالضوء Phototherapy

تطبيق المواد النانوية في مستحضرات التجميل Application of nanomaterials in cosmetics

سمية المواد النانوية Toxicity of nanomaterials

تطبيقات المواد النانوية في الأغشية Applications of nanomaterials in membranes

تأثير المواد النانوية على البكتريا الموجودة في الماء Effect of nanomaterials on bacteria in water

اسباب تلوث المياه Causes of water pollution

تطبيق المواد النانوية في معالجة المياه Application of nanomaterials in water treatment

مصير المواد النانوية في التربة Fate of nanomaterials in soil