ويستفاد من هذه العلاقة ≼ في المقارنة بين الأعداد الحقيقية ح وبما ان 5<3 فإن ( 5 – 3) < صفر موجب .

وبما ان 5>3 فإن ( 3 – 5 = -2)> صفر سالب .

ثم بما ان 5 =5 فإن ( 5 – 5 = صفر) = صفر صفر .

من هنا ينشأ قانون التثليث الذي مفاده باختصار شديد , لأي عددين حقيقيين س , ص

فإذا كانت س < ص فإن س – ص < صفر موجب .

هنا وإذا كانت س = ص فإن س – ص = صفر .

وإذا كانت س > ص فإن س – ص > صفر سالب .

وهذا القانون يرتب الأعداد الحقيقية على خط الأعداد عن طريق علاقة الترتيب كما يلي :

وهكذا عندما يمكن تمثيل كل عدد حقيقي بنقطة واحدة فقط على خط الأعداد هذا والعكس صواب أي ان كل نقطة على الخط تمثل عدداً حقيقياً واحداً فقط .

وأخيراً خط الأعداد هذا يقسم مجموعة الأعداد الحقيقية إلى ثلاث مجموعات هي وعلى الترتيب .

مجموعة الأعداد الحقيقية السالبة حَ وتمثل على يسار الصفر على خط الأعداد والصفر كمجموعة لوحده { 0} .

ثم مجموعة الأعداد الحقيقية الموجبة ح+ وتمثل على يمين على يمين الصفر على خط الأعداد وهناك رموز أخرى للتباين تنشأ من هذه العلاقة وعلاقة الترتيب وهي :

أكبر أو يساوي ←3≼5 والتفسير المنطقي 3<5) او 5=3)

أكبر من أو أصغر من 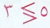 والتفسير المنطقي 3<5) او 5>3)

أكبر من أو يساوي أو أصغر من  والتفسير المنطقي 3<5) او5=3 او5>3)

مواضيع ذات صلة

Factors and Multiples

Basic Division

Addition

Division by Zero

Descartes and His Coordinate System

Decimals

Data Analyst

Coordinate System, Polar

Calculators

Bouncing Ball, Measurement of a

Angles, Measurement of

Angles of Elevation and Depression