Now, the next waves of interest, that are easily seen by everyone and which are usually used as an example of waves in elementary courses, are water waves. As we shall soon see, they are the worst possible example, because they are in no respects like sound and light; they have all the complications that waves can have. Let us start with long water waves in deep water. If the ocean is considered infinitely deep and a disturbance is made on the surface, waves are generated. All kinds of irregular motions occur, but the sinusoidal type motion, with a very small disturbance, might look like the common smooth ocean waves coming in toward the shore. Now with such a wave, the water, of course, on the average, is standing still, but the wave moves. What is the motion, is it transverse or longitudinal? It must be neither; it is not transverse, nor is it longitudinal. Although the water at a given place is alternately trough or hill, it cannot simply be moving up and down, by the conservation of water. That is, if it goes down, where is the water going to go? The water is essentially incompressible. The speed of compression of waves—that is, sound in the water—is much, much higher, and we are not considering that now. Since water is incompressible on this scale, as a hill comes down the water must move away from the region. What actually happens is that particles of water near the surface move approximately in circles. When smooth swells are coming, a person floating in a tire can look at a nearby object and see it going in a circle. So it is a mixture of longitudinal and transverse, to add to the confusion. At greater depths in the water the motions are smaller circles until, reasonably far down, there is nothing left of the motion (Fig. 51–9).

Fig. 51–9. Deep-water waves are formed from particles moving in circles. Note the systematic phase shifts from circle to circle. How would a floating object move?
To find the velocity of such waves is an interesting problem: it must be some combination of the density of the water, the acceleration of gravity, which is the restoring force that makes the waves, and possibly of the wavelength and of the depth. If we take the case where the depth goes to infinity, it will no longer depend on the depth. Whatever formula we are going to get for the velocity of the phases of the waves must combine the various factors to make the proper dimensions, and if we try this in various ways, we find only one way to combine the density, g, and λ in order to make a velocity, namely, 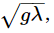 which does not include the density at all. Actually, this formula for the phase velocity is not exactly right, but a complete analysis of the dynamics, which we will not go into, shows that the factors are as we have them, except for
which does not include the density at all. Actually, this formula for the phase velocity is not exactly right, but a complete analysis of the dynamics, which we will not go into, shows that the factors are as we have them, except for  :
:

It is interesting that the long waves go faster than the short waves. Thus, if a boat makes waves far out, because there is some sports-car driver in a motorboat travelling by, then after a while the waves come to shore with slow sloshings at first and then more and more rapid sloshings, because the first waves that come are long. The waves get shorter and shorter as the time goes on, because the velocities go as the square root of the wavelength.
One may object, “That is not right, we must look at the group velocity in order to figure it out!” Of course that is true. The formula for the phase velocity does not tell us what is going to arrive first; what tells us is the group velocity. So we have to work out the group velocity, and it is left as a problem to show it to be one-half of the phase velocity, assuming that the velocity goes as the square root of the wavelength, which is all that is needed. The group velocity also goes as the square root of the wavelength. How can the group velocity go half as fast as the phase? If one looks at the bunch of waves that are made by a boat travelling along, following a particular crest, he finds that it moves forward in the group and gradually gets weaker and dies out in the front, and mystically and mysteriously a weak one in the back works its way forward and gets stronger. In short, the waves are moving through the group while the group is only moving at half the speed that the waves are moving.

Fig. 51–10. The wake of a boat.
Because the group velocities and phase velocities are not equal, then the waves that are produced by an object moving through are no longer simply a cone, but it is much more interesting. We can see that in Fig. 51–10, which shows the waves produced by an object moving through the water. Note that it is quite different than what we would have for sound, in which the velocity is independent of wavelength, where we would have wavefronts only along the cone, travelling outward. Instead of that, we have waves in the back with fronts moving parallel to the motion of the boat, and then we have little waves on the sides at other angles. This entire pattern of waves can, with ingenuity, be analyzed by knowing only this: that the phase velocity is proportional to the square root of the wavelength. The trick is that the pattern of waves is stationary relative to the (constant-velocity) boat; any other pattern would get lost from the boat.
The water waves that we have been considering so far were long waves in which the force of restoration is due to gravitation. But when waves get very short in the water, the main restoring force is capillary attraction, i.e., the energy of the surface, the surface tension. For surface tension waves, it turns out that the phase velocity is

where T is the surface tension and ρ the density. It is the exact opposite: the phase velocity is higher, the shorter the wavelength, when the wavelength gets very small. When we have both gravity and capillary action, as we always do, we get the combination of these two together:

where k=2π/λ is the wave number. So, the velocity of the waves of water is really quite complicated. The phase velocity as a function of the wavelength is shown in Fig. 51–11; for very short waves it is fast, for very long waves it is fast, and there is a minimum speed at which the waves can go. The group velocity can be calculated from the formula: it goes to 3/2 the phase velocity for ripples and 1/2 the phase velocity for gravity waves. To the left of the minimum the group velocity is higher than the phase velocity; to the right, the group velocity is less than the phase velocity. There are a number of interesting phenomena associated with these facts. In the first place, since the group velocity is increasing so rapidly as the wavelength goes down, if we make a disturbance there will be a slowest end of the disturbance going at the minimum speed with the corresponding wavelength, and then in front, going at higher speed, will be a short wave and a very long wave. It is very hard to see the long ones, but it is easy to see the short ones in a water tank.
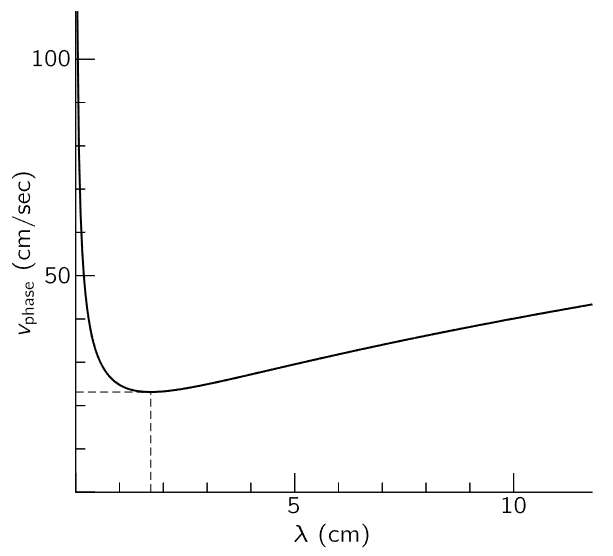
Fig. 51–11. Phase velocity vs. wavelength for water.
So, we see that the ripples often used to illustrate simple waves are quite interesting and complicated; they do not have a sharp wavefront at all, as is the case for simple waves like sound and light. The main wave has little ripples which run out ahead. A sharp disturbance in the water does not produce a sharp wave because of the dispersion. First come the very fine waves. Incidentally, if an object moves through the water at a certain speed, a rather complicated pattern results, because all the different waves are going at different speeds. One can demonstrate this with a tray of water and see that the fastest ones are the fine capillary waves. There are slowest waves, of a certain kind, which go behind. By inclining the bottom, one sees that where the depth is lower, the speed is lower. If a wave comes in at an angle to the line of maximum slope, it bends and tends to follow that line. In this way one can show various things, and we conclude that waves are more complicated in water than in air.
The speed of long waves in water with circulational motions is slower when the depth is less, faster in deep water. Thus, as water comes toward a beach where the depth lessens, the waves go slower. But where the water is deeper, the waves are faster, so we get the effects of shock waves. This time, since the wave is not so simple, the shocks are much more contorted, and the wave over-curves itself, in the familiar way shown in Fig. 51–12. This is what happens when waves come into the shore, and the real complexities in nature are well revealed in such a circumstance. No one has yet been able to figure out what shape the wave should take as it breaks. It is easy enough when the waves are small, but when one gets large and breaks, then it is much more complicated.

Fig. 51–12. A water wave.
An interesting feature about capillary waves can be seen in the disturbances made by an object moving through the water. From the point of view of the object itself, the water is flowing past, and the waves which ultimately sit around it are always the waves which have just the right speed to stay still with the object in the water. Similarly, around an object in a stream, with the stream flowing by, the pattern of waves is stationary, and at just the right wavelengths to go at the same speed as the water going by. But if the group velocity is less than the phase velocity, then the disturbances propagate out backwards in the stream, because the group velocity is not quite enough to keep up with the stream. If the group velocity is faster than the velocity of the phase, the pattern of waves will appear in front of the object. If one looks closely at objects in a stream, one can see that there are little ripples in front and long “slurps” in the back.
Another interesting feature of this sort can be observed in pouring liquids. If milk is poured fast enough out of a bottle, for instance, a large number of lines can be seen crossing both ways in the outgoing stream. They are waves starting from the disturbance at the edges and running out, much like the waves about an object in a stream. There are effects from both sides which produce the crossed pattern.
We have investigated some of the interesting properties of waves and the various complications of dependence of phase velocity on wavelength, the speed of the waves on depth, and so forth, that produce the really complex, and therefore interesting, phenomena of nature.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


